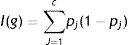En los estudios de casos y controles anidados, el muestreo de los controles se hace habitualmente por densidad de incidencia y mediante emparejamiento. Con respecto a los casos control clásicos, son más eficientes, permiten el cálculo de la incidencia de la enfermedad y cuentan con más validez interna por la menor presencia de sesgo. Las técnicas de riesgos competitivos pueden usarse si se estudian diferentes tipos de eventos y nos centramos en el tiempo y el tipo del primer evento. El particionamiento recursivo es un tipo de análisis multivariante cuyo propósito es la construcción de algoritmos de clasificación, especialmente útiles cuando hay un gran número de variables predictoras con relaciones complejas con el evento objeto de estudio.
In nested case-control studies, sampling of controls is usually done by density of incidence and pairing. With regard to the classic control cases studies, nested ones are more efficient, allow the calculation of the incidence of the disease and they have more internal validity due to the lower presence of bias. Competitive risks techniques can be used if we study different types of events and focus on the time and type of the first event. Recursive partitioning is a type of multivariate analysis whose purpose is the construction of classification algorithms, and it is especially useful when there are a large number of predictive variables with complex relationships with the event.
El proceso de la investigación en salud ha de iniciarse, como no podía ser de otro modo, en la definición del problema clínico que nos preocupa y que queremos solucionar. Aunque parezca obvio, a veces no lo es tanto el preguntarse qué quiero hacer, qué motivos me mueven a ello y si hay alguien antes que se haya hecho las mismas preguntas.
Es necesario contrastar que la información que pretendo aportar en relación al problema clínico que observo en mis pacientes de la UCI, con lo que ya hay en la literatura. Hay que ser consecuentes con la evidencia de que hay de algo y nuestro objetivo. Es decir, no parece pertinente en la actualidad hacer un estudio observacional sobre el efecto de un tratamiento antibiótico adecuado en la mortalidad de pacientes críticos con shock séptico. Uno tiene que pensar siempre en hacer estudios de calidad y con impacto, y esto no significa que obligatoriamente tengamos que hacer siempre estudios experimentales aleatorizados, pero lo que también carece de sentido es hacer la enésima cohorte descriptiva de limitado valor local. Otra cuestión importante es la ética, antes de plantearnos hacer un estudio debemos de tener en cuenta consideraciones éticas pues nunca hay que olvidar que la investigación finalmente va destinada a mejorar la calidad de vida de los pacientes, es decir, está fuera de toda duda la improcedencia de un ensayo clínico en el que pudiendo tratar adecuadamente a un grupo de pacientes dejáramos de hacerlo para observar si la mortalidad relacionada se ve incrementada.
Siguiendo el esquema del cuadro resumen abajo descrito, deberemos hacernos las mismas preguntas en función de las necesidades que va a plantear mi estudio:
- –
¿Voy a realizar alguna intervención?Por intervención no se ha de tener en cuenta solo la administración de tratamiento, puede ser una prueba diagnóstica, una medida preventiva, etc.
Sí → ensayo clínico (diseño experimental).
No→ estudio observacional.
- –
¿Los datos que voy a utilizar son de individuos o de grupo de individuos?Individuos → estudios individuales.Subgrupos de pacientes → estudios ecológicos.
- –
¿Tengo una hipótesis causal o necesito primero describir para establecer la hipótesis?Descriptivos → estudios transversales.Analíticos → estudios longitudinales.
- –
¿Cómo voy a medir la relación causal?Hacia delante → (exposición → efecto). Estudio de cohortes.Hacia atrás → (efecto → exposición). Estudio de casos y controles.
En este capítulo nos centraremos en algunos diseños avanzados y aún poco utilizados en la investigación clínica en general y en la realizada en las UCI en particular.
Estudios de cohortes y casos control. Estudios híbridosEn los últimos tiempos, se están abriendo paso algunos estudios que utilizan un diseño algo alejado de lo que más frecuentemente observamos en las publicaciones científicas. Quizás porque se busca paliar en la medida de lo posible las limitaciones de los métodos llamados clásicos y puede ser que también por el auge y el avance de estos métodos modernos y más robustos. Aunque seguramente sea por ambas causas. En el capítulo que nos ocupa, trataremos uno de ellos, incluido entre los comúnmente conocidos como estudio híbridos, que son los estudios de casos y controles anidados en una cohorte.
Dentro de la metodología de investigación, el apartado referente al diseño de estudios puede que sea de los más importantes porque, en resumidas cuentas, si queremos responder una pregunta de investigación surgida de la observación de nuestros pacientes, hemos de saber cómo diseñar un estudio adecuadamente para que las conclusiones a las que lleguemos al final tengan la validez necesaria. No basta con tener un interrogante al que dar respuesta, sino que deberemos saber qué diseño o tipo de estudio responde de forma adecuada a la misma.
Dado que los estudios de casos y controles anidados en una cohorte son una suerte de mezcolanza entre los estudios de cohortes y los de casos y controles, creemos que merece la pena contextualizar aquí ambos tipos de estudios.
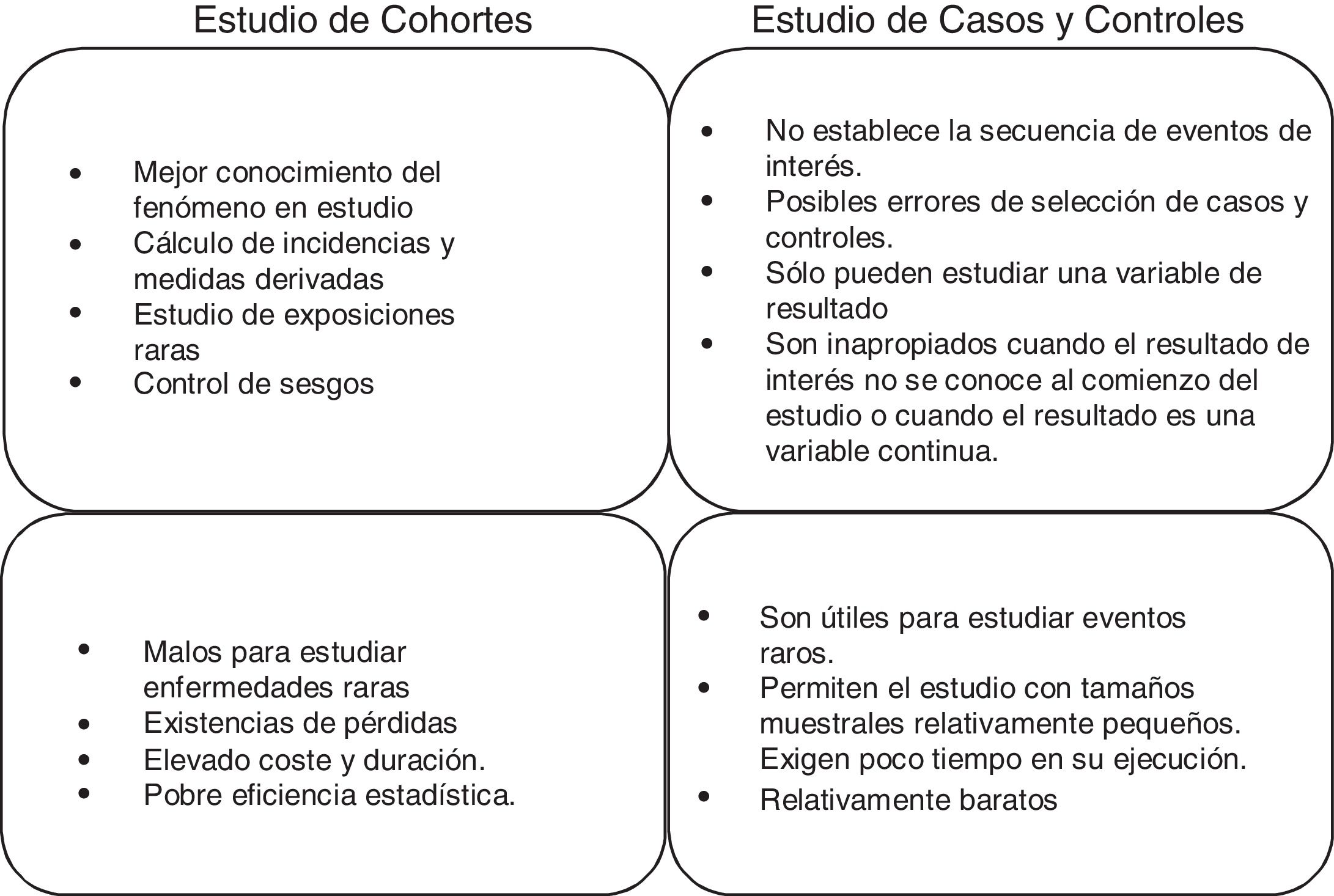
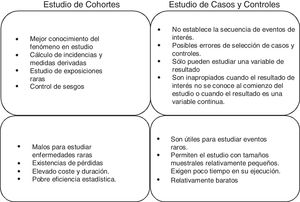
Estudios de cohortes y casos controlEstos 2 tipos de estudios son estudios observacionales de datos individuales, longitudinales y analíticos. O lo que es lo mismo, son estudios en los que no intervenimos, solo observamos qué ocurre; cada sujeto es una unidad del estudio que haremos a lo largo del tiempo para verificar una hipótesis causa-efecto. En la práctica, son los estudios más numerosos, ya que consiguen un buen nivel de evidencia sin necesidad de grandes recursos. Un buen resumen de las diferencias entre ambos tipos de estudios podría ser el mostrado en la figura 1.
Estudios de cohortesUna cohorte es un grupo de pacientes que comparten al menos una característica en común y que son observados durante un periodo, por ejemplo, pacientes diagnosticados de neumonía asociada a ventilación mecánica, pacientes con ictus isquémico con tratamiento anticoagulante y pacientes en shock séptico con hipoxia. Con este diseño se observa a pacientes que han estado o están expuestos a un determinado factor o circunstancia y se compara la prevalencia o incidencia de un determinado evento con respecto a otro grupo que no ha estado o no está expuesto al mismo factor. Por tanto, la cronología más lógica en el desarrollo de este tipo de estudios sería la que implica esa observación desde un momento dado en el tiempo y de ahí en adelante, siendo la consecuencia más ventajosa de este hecho la capacidad de calcular la incidencia de dicho evento y, por tanto, el riesgo relativo (RR) de ocurrencia del mismo entre expuestos y no expuestos1.
La utilidad que tienen los estudios de cohortes es que permiten verificar hipótesis causales. Es decir, permiten rechazar o aceptar una hipótesis planteada alternativamente a otra nula inicialmente aceptada hasta ese momento, por falta de elementos de juicio que nos permitan descartarla en favor de otra con más evidencia. De hecho, es el mejor diseño disponible para identificar asociaciones causales entre un factor de riesgo y una enfermedad (para el que no es posible realizar estudios experimentales). Sin embargo, la principal limitación que tienen es la comparabilidad de los grupos bajo estudio. Es decir, controlar si los 2 grupos que se comparan (expuestos versus no expuestos) son intercambiables.
Veamos un ejemplo. Supongamos que nuestra hipótesis es que la administración de antibioterapia apropiada previamente al ingreso en la UCI en pacientes con shock séptico reduce la mortalidad hospitalaria. Nuestra población de muestreo serían los pacientes que ingresan con una situación de shock séptico, la cual separamos en individuos que reciben antibioterapia adecuada antes del ingreso en la UCI e individuos que la reciben ya hospitalizados en la UCI. Hacemos seguimiento durante unos meses y finalmente comparamos la mortalidad hospitalaria en ambos grupos. El principal defecto del estudio es que no sabemos si el grupo de los que son tratados antes de la UCI es idéntico al de los que son ya ingresados en la UCI, o lo que es lo mismo, ¿está el hecho de recibir antibioterapia adecuada antes de la UCI influido por otra variable que no estamos teniendo en cuenta?
Dentro de los estudios de cohortes, en función del momento de inclusión, podemos encontrar cohortes fijas o dinámicas; en función de la selección de las cohortes, éstas pueden ser de comparación interna o externa y, según el inicio del estudio, pueden ser prospectivas o retrospectivas. Una cohorte retrospectiva no significa que el sentido cronológico sea desde la aparición del Evento al estudio del Factor (E > F), sino que la información se recupera del pasado y no desde el momento actual1.
Estudios de casos y controlesLos estudios de casos controles son un diseño epidemiológico analítico no experimental, es decir, basado en la observación, a priori más eficiente en la verificación o contraste de hipótesis. En este tipo de estudio se parte del efecto o evento y se pretende estudiar sus antecedentes. Para ello, se seleccionan 2 grupos de pacientes, llamados casos y controles, según aparezca o no el efecto (enfermedad, muerte u otro). Los grupos se comparan respecto a las exposiciones o características previas para esclarecer si están o no asociadas con el efecto objeto de estudio. Por lo tanto, la cronología más común de la observación es la que tiene en cuenta la exposición o característica precedentes y, a partir de ellas, intentar esclarecer si están asociadas o no con el efecto objeto de estudio. Y por ello este diseño no permite calcular la incidencia ni el RR, salvo en poco frecuentes situaciones.
En cambio, la medida de asociación empleada en estos estudios es la odds ratio (OR) o razón de ventajas o razón de oportunidades. Se podría entender esta medida como el cociente entre la proporción de los pacientes que presentan antecedentes de una exposición al factor en estudio y la proporción de aquellos que no tienen esa exposición previa. En otras palabras, si no hay asociación entre exposición y efecto no tendríamos ninguna razón para pensar que esa exposición apareciese diferentemente entre casos y controles, y por tanto la OR sería igual a 1.
Como desventajas más llamativas podríamos destacar que son más vulnerables a la presencia de determinados errores sistemáticos o sesgos, no detectan asociaciones débiles entre exposición y respuesta, o que puede resultar difícil, y a veces casi imposible, validar la información obtenida sobre la exposición.
En la práctica, los estudios de casos y controles surgen porque tenemos una serie de casos y queremos analizar los factores predisponentes que han generado dichos casos, mediante la comparación con una población control. La idea que no se nos puede olvidar es que tanto casos como controles deben de provenir de una misma cohorte original, de tal forma que si esta condición no se cumple, es decir, casos y controles representan a poblaciones distintas, se produce lo que se conoce con el nombre de sesgo de Berkson2.
El término control se utiliza en epidemiología experimental para el grupo que recibe el tratamiento convencional o placebo, aunque debe recordarse que los estudios de casos y controles son de tipo observacional, que no deben confundirse con los ensayos clínicos o de intervención (fig. 2).
Por ejemplo, tengo una serie de casos de pacientes críticos con infección nosocomial por un germen poco frecuente, tipo Klebsiella pneumoniae carbapenemasa (KPC) y queremos estudiar los factores de riesgo asociados a dicha infección. ¿Cuáles serían nuestros controles?
- a.
Cualquier paciente de la UCI sin infección nosocomial.
- b.
Pacientes con infección nosocomial por otros gérmenes.
- c.
Pacientes con el mismo rango de edad y sexo.
La respuesta correcta sería cualquier paciente de UCI, ya que cualquier paciente del hospital sería susceptible de presentar la infección nosocomial pero no la ha presentado. Tanto casos como controles vienen de la misma cohorte originaria, que son pacientes hospitalizados en la UCI.
Estudios de casos control anidados en una cohorteDescritos brevemente los estudios de cohorte y de casos y controles, es conveniente resaltar que los estudios de casos y controles anidados en una cohorte pertenecen a los comúnmente conocidos como estudio »híbridos», ya que tienen características tanto de los estudios de cohortes como de los de casos y controles, pero obviando algunas de sus limitaciones.
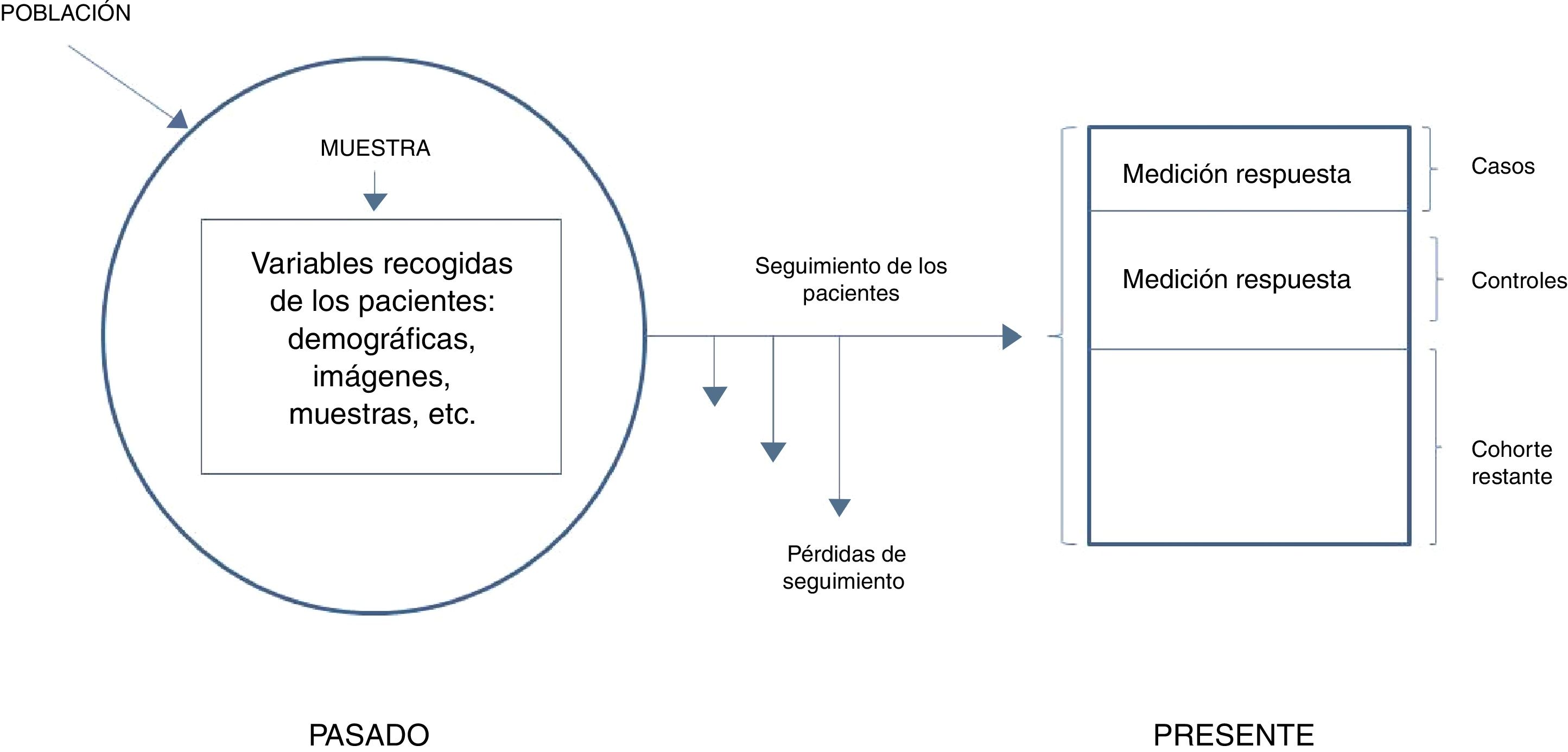
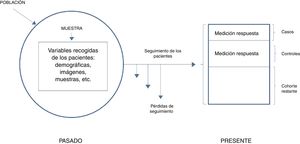
El primer estudio híbrido que se conoce fue publicado en 1962 para analizar la relación entre la exposición in útero a los rayos X y el riesgo posterior de cáncer3. Los estudios anidados se caracterizan por analizar todos los casos aparecidos en una cohorte estable seguida en el tiempo y utilizar como controles solo una muestra de los sujetos de esa misma cohorte. Es habitual que el investigador cuente con una cohorte que ha venido estudiando y siguiendo durante un periodo determinado, ha recopilado datos de diversa índole, guardado pruebas de imagen y/o muestras con el propósito de hacer un estudio futuro cuando observe respuestas inesperadas en esos pacientes. Es decir, se cuenta con información sobre la posible exposición y al producirse la respuesta ya tenemos datos con los que trabajar para determinar posibles relaciones causales.
En otras palabras, se observa una población dinámica (aquella en la que se asume estabilidad en las incorporaciones y salidas de individuos) para detectar todos los casos de la enfermedad diana. Estos casos son comparados con un grupo de referencia (no tendrían por qué ser controles entendidos como hasta ahora) seleccionados aleatoriamente o por emparejamiento de la misma población en la que se han originado los casos4.
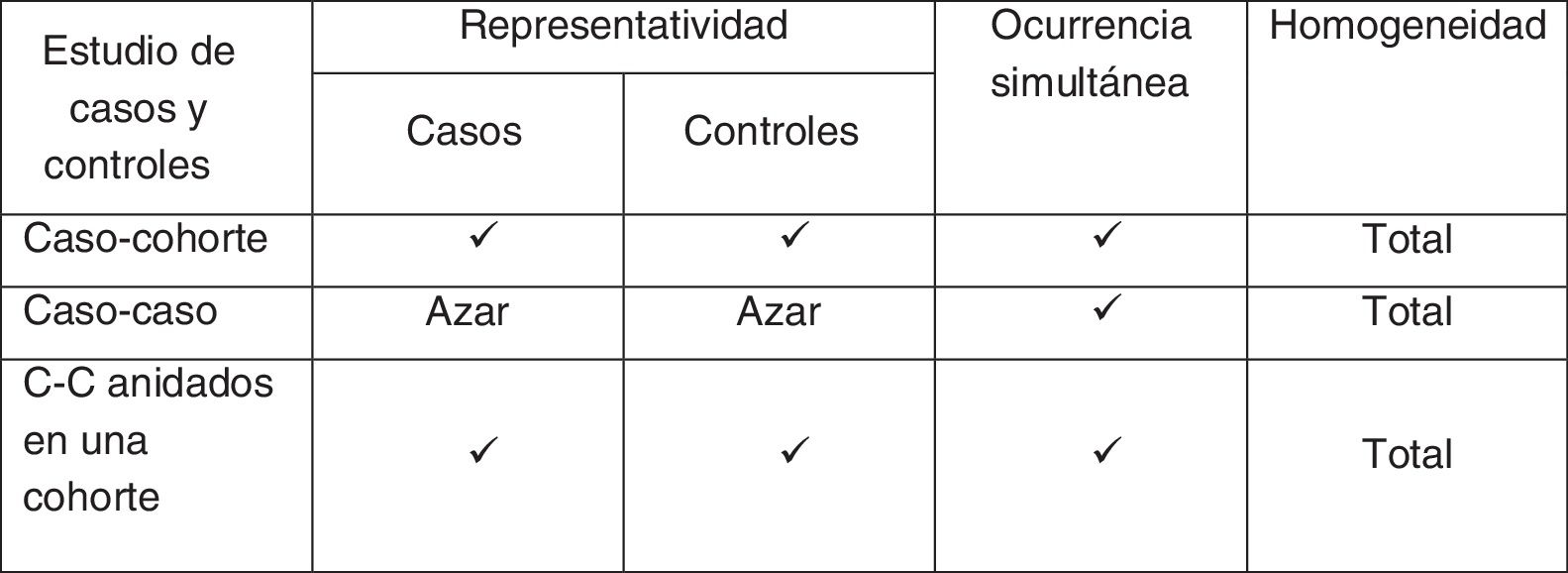
En términos generales, podríamos diferenciar entre 2 tipos de estudios anidados: los simples y los que utilizan la densidad de incidencia. Y ambos casos podrán ser tanto diseños prospectivos como retrospectivos. En el primer caso, la respuesta es poco frecuente y con una medición inicial de la exposición es suficiente. El investigador, en primer lugar, identifica a todos los participantes de la cohorte que presenten la respuesta al final del periodo de seguimiento (casos) y después define una muestra aleatoria de aquellos que no la hayan presentado (controles). Después analiza las variables predictivas en ambos grupos y compara los niveles o las categorías del factor de riesgo en los casos frente a los controles. En el caso de estudios con densidad de incidencia, puede ocurrir que el seguimiento sea variable, o que la exposición varíe a lo largo del tiempo. Son por ello cohortes dinámicas y el muestreo de los controles se hace por densidad de incidencia y mediante emparejamiento, por lo que hay que esperar a que se hayan producido todos los casos para seleccionar toda la población de referencia. Ahora la medición en un único punto no será suficiente y deberemos de tener en cuenta que los controles habrán de ser seleccionados como individuos pertenecientes a la misma cohorte e igualmente expuestos que los casos, es decir, en riesgo, pero que aún no han mostrado respuesta. En este diseño, debido a que los controles son, en definitiva, pacientes procedentes de la cohorte inicial, perdemos precisión estadística, aunque este hecho se ve en parte compensado por la reducción en el número de sujetos estudiados y el menor coste de la recogida de datos y un seguimiento usualmente más reducido (fig. 3).
Casos y controles anidados simple.
Adaptada de Hulley5, 2014.
Debido a que en los estudios de casos y controles anidados la información sobre los factores de riesgo de interés y las variables principales se han recogido al inicio del seguimiento, de forma prospectiva y antes de que se desarrolle la enfermedad, hay menos riesgo de que se produzcan los sesgos de información clásicos de los estudios de casos y controles, de naturaleza retrospectiva.
Se parte de una cohorte inicial amplia que, como hemos comentado, muchas veces está disponible de estudios anteriores, con la que se realiza un diseño sintético de casos y controles para reducir el número de sujetos sobre los que tengamos que manejar variables independientes o covariables (y no considerar para el análisis estadístico las de toda la cohorte). La selección de los casos es inmediata puesto que se trata de nuestros enfermos. Primero hemos de identificarlos asumiendo una definición de caso lo más homogénea posible. La única particularidad es recoger todos los casos durante un periodo determinado y en una colectividad definida. Además, dado que la incidencia de la mayor parte de las enfermedades que se estudian es relativamente baja, interesa seleccionar todos los casos que aparecen en la cohorte, aunque podría utilizarse cualquier otra fracción de muestreo.
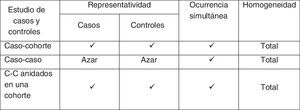
De hecho, según el método de muestreo empleado a partir de los pacientes individuales de la cohorte inicial que dé como resultado la formación de los 2 grupos, tendremos diferentes tipos de diseños híbridos: estudios de casos y controles anidados dentro de una cohorte, y estudios de cohorte y casos. En el caso de los estudios de casos y controles anidados en una cohorte, se utiliza un esquema de muestreo conocido como de grupo de riesgo, ya que la selección de un individuo como control depende de que este se encuentre en riesgo, es decir, sea miembro de la cohorte en el momento en que se selecciona o identifica el caso. Los casos y el conjunto de individuos en riesgo que no desarrollaron el evento constituyen el grupo de riesgo.
Selección de controlesCon respecto a la selección de los controles en estos estudios anidados, es asumible el método que comentamos para los estudios de casos y controles clásicos. Es conveniente emparejarlos teniendo en cuenta variables de confusión y dependientes del tiempo como, por ejemplo, los años que llevan incluidos en la cohorte. De esta forma, un mismo sujeto puede actuar como control en varias ocasiones y terminar como caso en otra, lo que habrá de tenerse en cuenta a la hora del análisis estadístico de los estudios. Además, el emparejamiento por variables dependientes del tiempo limita el análisis de dichas variables en estos diseños híbridos anidados, aunque si la exposición es dependiente del tiempo, estos estudios no necesitan recoger información más allá del momento de la selección de los casos.
Aunque lo habitual es seleccionar un control por cada caso, en caso de que la casuística del estudio sea baja podremos seleccionar más de un control por cada caso en aras de aumentar la potencia estadística del estudio, siempre que no se supere una proporción de 4:1 (4 controles por cada caso).
El emparejamiento es un método de comprensión relativamente sencilla y que presenta algunas ventajas importantes. Entre ellas están la capacidad de balancear casos y controles en cada estrato de la variable por la que se aparean, de forma que si el apareamiento es perfecto (si son dicotómicas o cuantitativas en las que se usa el mismo dintel para aparear), el control de la confusión es casi completo. Además, permite detectar interacciones entre la exposición y el factor usado para aparear. Por el contrario, adolece de algunas limitaciones, entre las que cabe destacar que se trata de un método que requiere trabajo y, por tanto, consume mucho tiempo, siendo además los test estadísticos específicos de datos apareados de aplicación imprescindible. La complejidad del análisis aumenta en consecuencia y casi nunca en paralelo a un aumento de la precisión en la estimación de los parámetros. Además, si la variable que se usa para emparejar no es confusora, la estimación final será poco precisa. Junto a estos inconvenientes, el desarrollo de modelos de regresión multivariante ha desplazado a un segundo plano el emparejamiento como sistema de control de la confusión.
Medidas de asociación en estudios de casos y controles anidadosAl contrario que en los estudios de casos y controles clásicos, en los estudios anidados, al estar los casos identificados a priori y ser registrados a medida que aparece la respuesta o la enfermedad de estudio, la incidencia medida como densidad puede calcularse sin problemas y, por tanto, esto nos permitirá estimar riesgos relativos. Esta es una diferencia importante con los estudios de casos y controles convencionales, en los que suele calcularse como medida de asociación la OR, que solo puede asemejarse al RR cuando la prevalencia del efecto es muy reducida, de forma que la diferencia entre OR y RR será mayor a más incidencia de la enfermedad en estudio6,7.
Por ejemplo, si quisiéramos estudiar la infección nosocomial en una UCI, proceso frecuente con una prevalencia según la epidemiología local de más del 20%, el diseño anidado no sería el más adecuado para estudiar los factores de riesgo de la infección por la fuerte distorsión entre OR y RR, aunque podría serlo para estudiar la prolongación de la estancia debido a la misma.
Estas características han de tenerse en cuenta en el análisis, que es algo más complicado pero con la ventaja de que la OR es siempre un estimador estadísticamente no sesgado de la razón de riesgos, o de tasas. Además, son muy eficientes para analizar un factor de riesgo, o controlar un factor de confusión, si no se dispone de la información necesaria para toda la cohorte, o aun teniéndola, si obtenerla es muy caro, como ocurre si hay que hacer determinaciones en muestras biológicas.
Para realizar un estudio de casos y controles anidado, en primer lugar se define la cohorte inicial de pacientes que se van a estudiar y se establece el periodo en riesgo. A continuación, se identificarían los casos, incluyendo las fechas de aparición, y posteriormente se obtiene una muestra de controles emparejados para cada uno de los casos. Finalmente, se definen y se cuantifican las variables predictivas. Es evidente, que al usar este tipo de selección, un sujeto inicialmente identificado como control podría desarrollar el evento de interés durante el seguimiento y posteriormente ser seleccionado como caso. De existir en alguna medida sesgo de selección, el que los controles sean elegidos a posteriori como casos compensa en cierta medida ese sesgo. En cualquier caso, esta situación no es fuente de error o de sesgo, ya que en los estudios de cohorte un mismo individuo puede contribuir tanto al numerador como al denominador, y esta misma situación se mantiene en este tipo de estrategia.
Aplicación práctica en la investigación en cuidados intensivosLa aplicación de este tipo de diseño se recomienda para el estudio de enfermedades poco frecuentes en cohortes dinámicas en las que la determinación de la exposición y sus cambios en el tiempo, en todos los miembros de la cohorte, resultaría muy costosa.
Otra situación en la que se recomienda la utilización de este diseño es aquella que precisa determinaciones costosas. Un ejemplo podría ser su utilización en una línea de investigación fundamental en los últimos tiempos, que es la que bascula en torno a la construcción de modelos predictivos que nos permitan conocer lo más precozmente posible las probabilidades de desarrollar ciertos síndromes o patologías directamente relacionadas con un mal resultado clínico de nuestros pacientes. Se trata del estudio de diferentes biomarcadores, como indicadores de riesgo, diagnósticos o pronósticos. Su utilización se está poniendo de relieve, con especial énfasis en el área de los cuidados críticos, fundamentalmente debido a la posibilidad que nos ofrecen de saber de manera poco invasiva, la predisposición de los pacientes a desarrollar determinados acontecimientos como la sepsis, o de cómo se relaciona su medida en ciertos momentos con «outcomes» clínicos de suma importancia, como la mortalidad en la UCI8-10.
Un caso práctico de aplicación de este tipo de diseño anidado en una UCI lo constituye el estudio de los factores de riesgo de reingreso en UCI tras su estancia inicial en pacientes receptores de trasplante hepático que realizó un grupo canadiense recientemente11.
En él, los autores emplean un diseño de casos y controles anidados en una cohorte de pacientes trasplantados hepáticos en el que a cada caso, es decir, a cada paciente trasplantado que ha de reingresar en la UCI, se le asigna de forma aleatoria un control que forma parte de la cohorte. La cohorte en este caso estaría constituida por todos los pacientes trasplantados en el periodo de estudio, que en este caso fue de 7 años. Como hemos comentado, este tipo de diseño se emplea en el estudio de eventos poco prevalentes.
Tras el análisis de los datos, la comparación estadística entre los casos (pacientes con readmisión en la UCI) y los controles (pacientes sin necesidad de readmisión en la UCI), los autores concluyen que el reingreso en la UCI tiene un impacto negativo en el resultado clínico de estos pacientes y exponen además qué factores están relacionados con esta necesidad de reingreso12.
Otro ejemplo de aplicación de este tipo de diseño híbrido podría ser el estudio de las consecuencias de la embolización mesentérica tras intervención endovascular aorto-ilíaca. En este ejemplo, los autores seleccionan los controles aleatoriamente pero apareando adicionalmente por edad y sexo12.
Como comentario final, los estudios de casos y controles anidados se parecen más al de casos y controles clásico que al de cohortes. La diferencia fundamental entre los 2 es que en el estudio anidado el muestreo de los controles se hace habitualmente por densidad de incidencia y mediante emparejamiento. Son más eficientes, permiten el cálculo de la incidencia de la enfermedad y cuentan con más validez interna por la menor presencia de sesgo.
Análisis de eventos competitivosIntroducción al riesgo competitivoEn los estudios de evaluación prospectiva, el resultado se obtiene de una evaluación longitudinal de una cohorte de sujetos en un tiempo hasta que se produce el fenómeno de interés, al que se denomina evento. Por ejemplo, el evento de interés puede ser el fallecimiento, un infarto de miocardio o la recurrencia de la enfermedad. El análisis estadístico utilizado para la estimación de estos resultados se denomina análisis de tiempo hasta el evento o, más comúnmente, análisis de supervivencia. El método más frecuente para estimar la probabilidad de un evento es el enfoque no paramétrico, generalmente denominado método de Kaplan-Meier (KM).
Las estimaciones del método KM analizan a los sujetos a los que le aparece un evento en un tiempo determinado y los sujetos que no presentan el evento y no completan el seguimiento son los que se denominan casos censurados, puesto que no presentan el evento de interés. No es infrecuente que un participante de un estudio experimente más de un tipo de evento durante el seguimiento. Se produce una situación de riesgos competitivos (RC) cuando la aparición de un tipo de evento modifica la capacidad de observar el evento de interés objeto de estudio.
Un ejemplo claro sería que el evento a evaluar fuese la supervivencia de los pacientes tras el recambio valvular en cirugía cardíaca como tratamiento de una endocarditis infecciosa y el RC en este caso es presentar un ictus durante el ingreso, puesto que estos pacientes no pueden ser intervenidos.
Hay muchos ejemplos en la literatura de la utilización de estas técnicas de RC8,13-15 pero la principal cuestión que debe plantearse el investigador es si tener o no en cuenta los RC. Cuando no se tienen en cuenta, el análisis se reduce al análisis habitual de tiempo hasta evento. Sin embargo, con esta aproximación, se está sobreestimando la probabilidad real16-20. La magnitud de esta sobreestimación es la que nos hará pensar en si incluirlo como RC o no.
Volviendo al ejemplo anterior la mortalidad tras la cirugía cardíaca como tratamiento de la endocarditis está en el 40%, pero hay un 25% de pacientes que antes de la cirugía tienen complicaciones neurológicas, lo que indica que la estimación puede ser muy diferente de la observada.
Cálculo de la cummulative incidence funtionCuando nos encontramos datos con RC es fundamental estimar el riesgo absoluto de la ocurrencia de un evento de interés hasta un punto t de tiempo de seguimiento. Este riesgo se calcula mediante la función de incidencia acumulada, cummulative incidence funtion (CIF), que se define para cada tipo de evento por separado y aumenta con el tiempo. La CIF de un evento en el tiempo t se define como la probabilidad de que un evento de ese tipo ocurra en cualquier momento entre la línea de base y el tiempo t. Si los datos no contienen a individuos censurados, la CIF en el tiempo t puede estimarse como la proporción del número de sujetos que experimentaron ese tipo de evento hasta el tiempo t dividido por el número total de sujetos en el conjunto de datos. A medida que el tiempo aumenta, el CIF aumenta de cero a la proporción total de eventos de ese tipo en los datos.
Modelización y efecto de las covariablesPara valorar el efecto de las covariables y un evento de interés, en ausencia de RC esto se realiza mediante los modelos de riesgos proporcionales de Cox21. En presencia de RC, los modelos de Cox son difíciles de interpretar.
Se han propuesto varios modelos de regresión en el CIF y el modelo más popular es el modelo de Fine y Gray22, que también se ha implementado en los paquetes de software estadístico más importantes, incluyendo R, STATA y SAS23,24. La medida de efecto resultante para cada covariable se denomina proporción de riesgo de subdistribución (sHR). Mientras que la interpretación numérica de sHR no es directa, un sHR=1 implica que no existe ninguna asociación entre la covariable y el correspondiente CIF, un sHR>1 implica que un aumento del valor de la covariable se asocia a un mayor riesgo, mientras que un sHR<1 implica lo contrario. Además, cuanto más lejos está el sRH de 1, mayor es el tamaño del efecto estimado en el CIF. El supuesto de proporcionalidad de los riesgos a lo largo del tiempo de seguimiento continúa siendo una exigencia.
Aspectos claves- 1.
Los RC ocurren si durante el tiempo de observación para un evento específico que es de interés pueden surgir otros eventos que modifiquen la ocurrencia de ese evento. De manera más general, los métodos de RC pueden usarse si se estudian diferentes tipos de eventos y se centra en el tiempo y el tipo del primer evento.
- 2.
La estadística descriptiva básica de los datos de RC es la CIF, que describe el riesgo absoluto de un evento de interés a lo largo del tiempo. El método KM no debe usarse en presencia de eventos competidores, ya que sobreestima el verdadero riesgo absoluto.
- 3.
Una complicación de los RC es que las covariables pueden afectar al riesgo absoluto y a la tasa de un evento de interés de manera diferente. Los modelos de regresión basados en el CIF (p. ej., los modelos Fine-Gray) exploran la asociación entre las covariables y el riesgo absoluto y, por lo tanto, son esenciales para la toma de decisiones médicas y las preguntas de investigación pronóstica. Por otra parte, se deben preferir modelos específicos de tasas de eventos (p. ej., modelos proporcionales de riesgos específicos de Cox) para responder a preguntas de investigación etiológicas.
- 4.
Una descripción completa de los datos de RC debe incluir el modelado de todos los tipos de eventos y no solo del evento de interés principal.
- 5.
Los modelos de RC pueden evaluar el efecto de una intervención sobre los componentes individuales de un criterio de valoración compuesto.
El particionamiento recursivo es un tipo de análisis multivariante cuyo propósito es de la elaboración de algoritmos de clasificación. Este tipo de algoritmos fueron publicados por primera vez en 196325 y a partir de ellos surgen distintos algoritmos en estos más de 50 años26. De todos ellos, el más utilizado en el campo de la salud es el introducido por Breiman et al. en 198427. Con estas herramientas podremos clasificar observaciones y desarrollar sistemas de predicción según un conjunto de reglas de decisión.
Este tipo de algoritmos son útiles cuando el evento estudiado tiene un gran número de variables predictoras y existen complejas relaciones entre ellas, llegando a ser muy empleados en la bioinformática y los estudios genéticos28.
Construcción de un árbol de clasificaciónLos árboles de clasificación y regresión son un procedimiento no paramétrico de predicción de una variable dependiente o respuesta sobre la base de un conjunto de predictores o variables independientes. La respuesta puede ser categórica.
El árbol se construye mediante la división recurrente de los datos. Esta división de la población tiene como objetivo hacer subpoblaciones homogéneas en relación con la variable dependiente. Estas particiones se vienen repitiendo de forma sucesiva hasta que el grado de homogeneidad ya no se puede incrementar con un nueva partición29. La elección de la variable para realizar la partición siempre se hará mediante un criterio de homogeneidad de las subpoblaciones resultantes al hacer la partición. La completa homogeneidad de los nodos es un objetivo que raramente se consigue, pero existen funciones que determinan el grado de impureza como medida del grado de homogeneidad de los nodos.
El índice de Gini es una de las funciones más habitualmente utilizadas para medir la homogeneidad de un nodo en los árboles de clasificación, de tal forma que para una variable resultado con «c» clases distintas la impureza de un nodo g se define:
donde pj es la proporción de individuos en la clase j en el nodo g. Esto lo veremos mejor con un ejemplo.
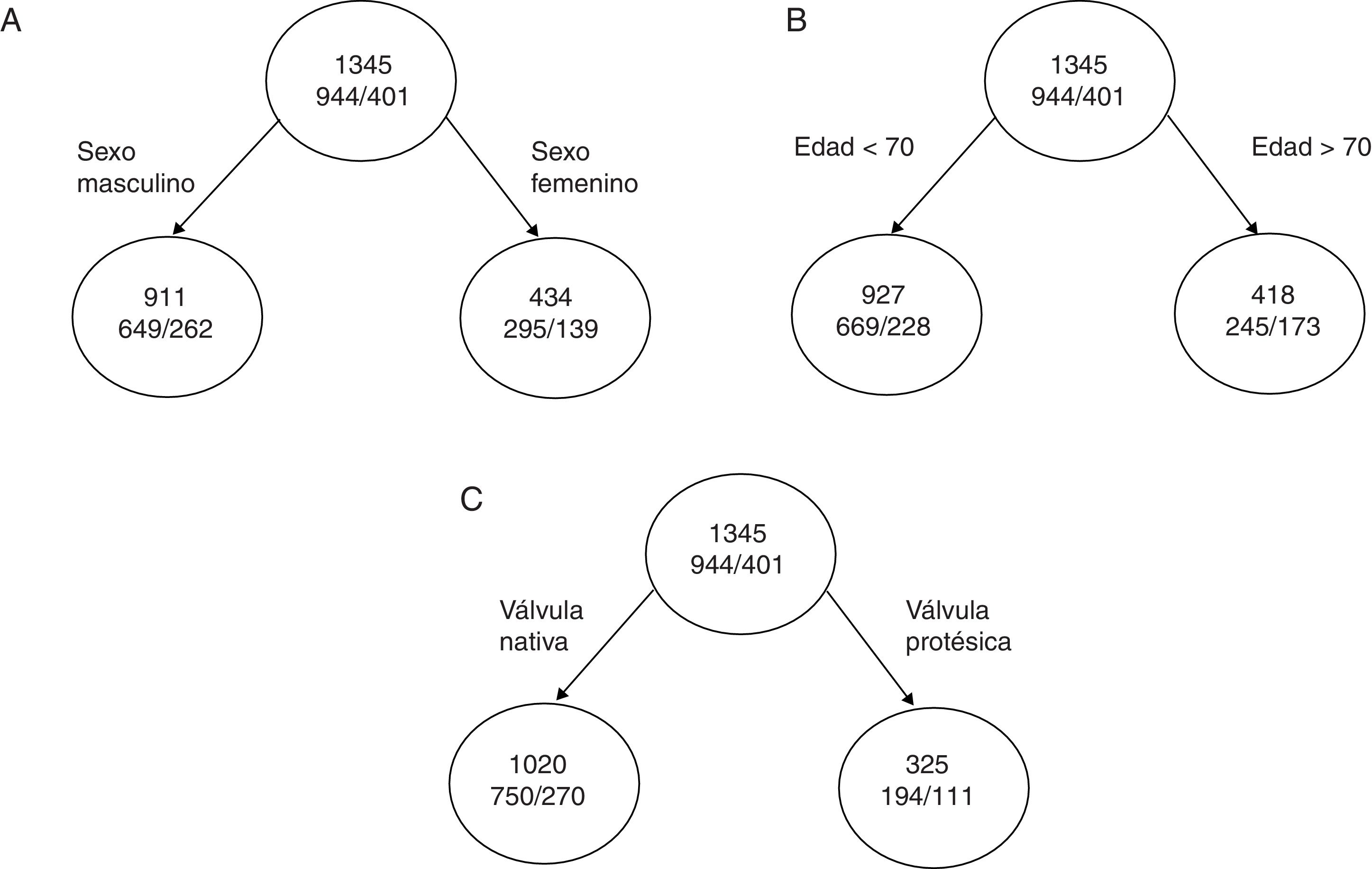
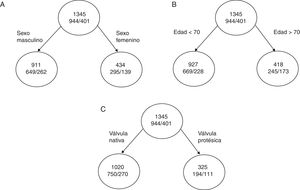
Veamos un caso práctico; si hablamos sobre la mortalidad total de una serie de pacientes con endocarditis infecciosa30, tenemos 3 variables en función de las cuales podríamos clasificar la mortalidad de los pacientes y estas son la edad, el sexo y el tipo de válvula afecta (nativa/protésica). La mortalidad total de la cohorte es del 29,8% (401/1345). La mortalidad por sexo hombre es del 29%, la mortalidad de los pacientes mayores de 70 años es del 41% y la mortalidad de los pacientes con endocarditis sobre válvula protésica es del 40%.
Si dividimos el nodo inicial como está representado en la A y la impureza de cada nodo es:
I(inicial)=0,70×(1-0,70)+0,30×(1-0,30)=0,42
I(masculino)=0,71×(1-0,71)+0,29×(1-0,29)=0,410
I(femenino)=0,68×(1-0,68)+0,32×(1-0,32)=0,435
por lo tanto, la reducción de la impureza de esta partición es de:
ΔI=1345×I(inicial) –(911×I[masculino]+434×I[femenino])=0,87
Siguiendo con los otros dos ejemplos (fig. 4 B y C), la reducción de la impureza es de:
ΔI (edad)=1,98 ΔI (válvula)=14,55
Podemos comprobar como con porcentajes de mortalidad similar, el dividir el árbol por la variable del tipo de válvula afectada reduce mucho más la impureza y aumenta el poder de clasificación.
Número de nodosUna de las cuestiones más importantes es determinar el número final de particiones de un árbol o, lo que es lo mismo, determinar el tamaño del árbol. Si el proceso de división termina demasiado pronto, no habremos obtenido todo el poder clasificatorio del árbol, cometiendo un subajuste. Por el contrario, si se realizan demasiadas divisiones, corre el riesgo de clasificar particularidades azarosas de los datos; es lo que se conoce como sobreajuste.
Para llegar al tamaño correcto del árbol, lo que se conoce como árbol honesto (honest tree), hay que modelizar la muestra en varios intentos para llegar a este punto óptimo.
Ventajas y desventajas respecto a otros modelos multivarianteVentajas- –
Genera modelos clínicamente más intuitivos31.
- –
Permite variar el orden de clasificación para crear reglas de decisión con mayor sensibilidad y especificidad32, ya que permiten identificar relaciones no lineales con las variables dependientes.
- –
Puede ser más preciso y especialmente útil en identificar interacciones que puedan ser incluidas en modelos multivariantes33.
- –
No funciona para variables continuas que habría que dicotomizar; sí sirve para elegir el punto de corte más adecuado como alternativas a las curvas ROC34.
- –
Sobreajuste de los datos.
Los autores declaran no tener ningún conflicto de intereses.