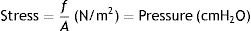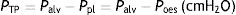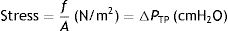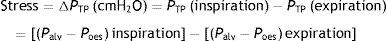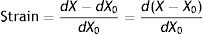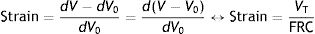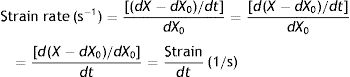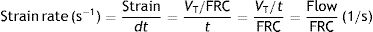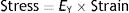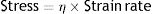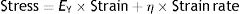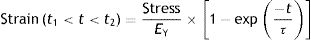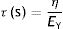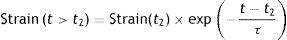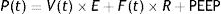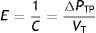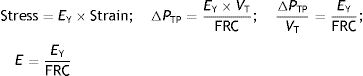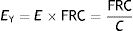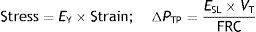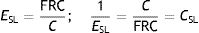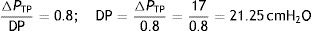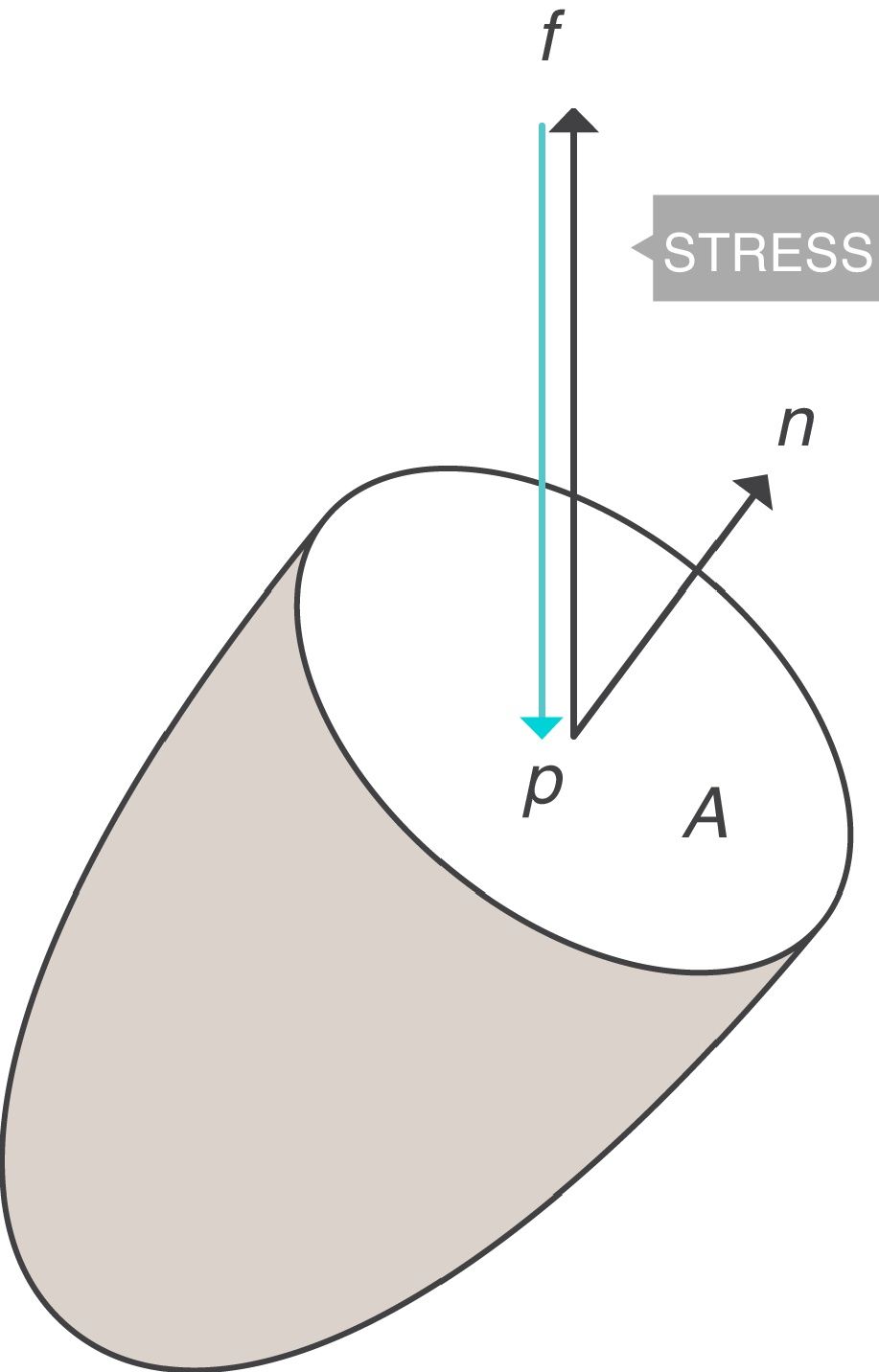
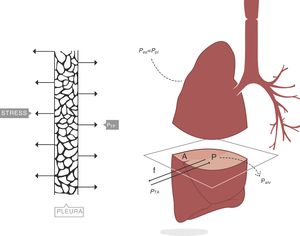
Consider point p in the inside of a body, and a plane (A) corresponding to the cross section surface of the body taken at point p (Fig. 1) (3), If a force f is then applied to this body, then stress applied to the material can be defined as:

Figure 1.

Stress=pressure. Source: Reproduced with permission Modesto-Alapont et al.5

(0.04MB).

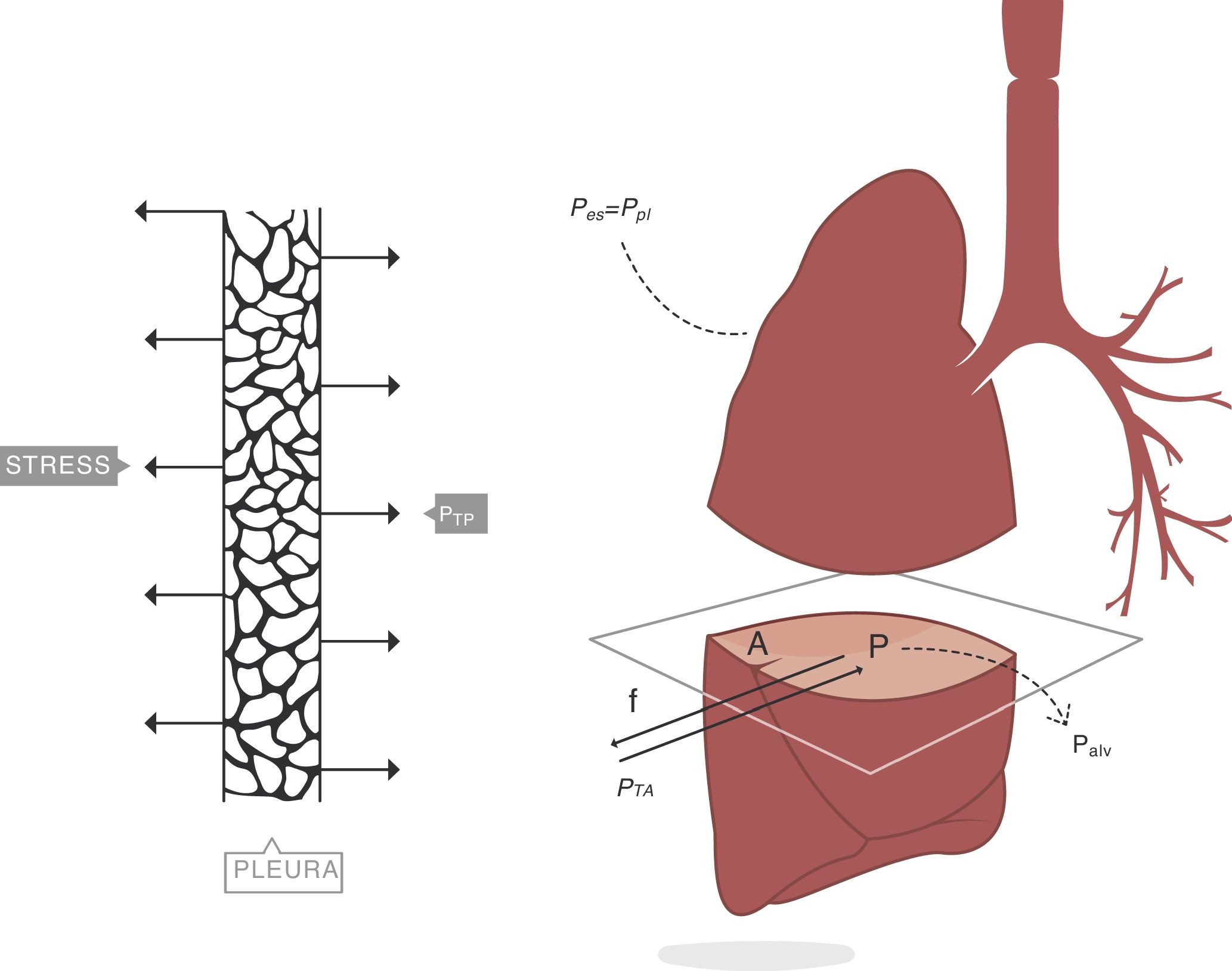
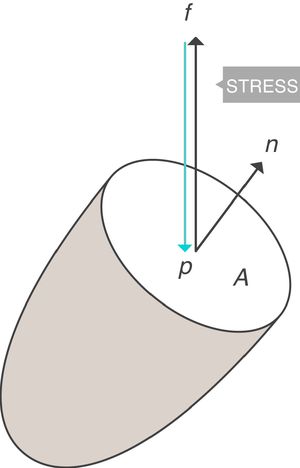
When applying the concept above to the lung (4), it is possible to study a cross section (A) which includes lung parenchyma surrounded by pleura. In the lung, transpulmonary pressure (PTP) or retraction pressure of the lung is defined by the difference between intra-alveolar pressure (Palv) and pleural pressure (Ppl). In a bedside situation Ppl can be measured by estimating the pressure in the mediastinum such as within the oesophagus (Poes) (Fig. 2). So:

Figure 2.

Transpulmonary pressure (PTP)=retraction pressure of the lung. A: surface A; P: point P; f: force; Palv: alveolar pressure; Ppl: pleural pressure; Poes: oesophageal pressure. Source: Reproduced with permission Modesto-Alapont et al.26

(0.13MB).

PTP is a vector with the same intensity (modulus) but in the opposite direction to the retraction force of the lung, i.e. PTP represents this retraction force. This is the reason why PTP can also be referred to as the retraction pressure of the lung.

The force that causes the lungs to inflate and deflate, therefore changing the lung volume, is the change in transpulmonary pressure (ΔPTP).5 Therefore, the rheological concept of stress applied to lung tissue when there is a change in volume can be expressed by:

PTP is a static measurement which should be measure in the absence of flow. Both inspiratory (Pinsp) and expiratory (Pexp) values are measured by inspiratory pause and expiratory pause maneouvres.

If the movement of the lung is studied when filling with air, it can be observed that it starts from one rest position (PTP of the end-expiratory volume) and at the end of inspiration, the lung returns to another rest position (PTP of the end-inspiratory volume). Therefore, during inspiration the stress increases in magnitude and reaches a maximum (= f/dA) in the inspiratory pause (Pplat). At these rest points the total force applied on the lung must be zero otherwise the lung would continue to inflate. This is exactly the opposite process which occurs during expiration when the lung deflates.

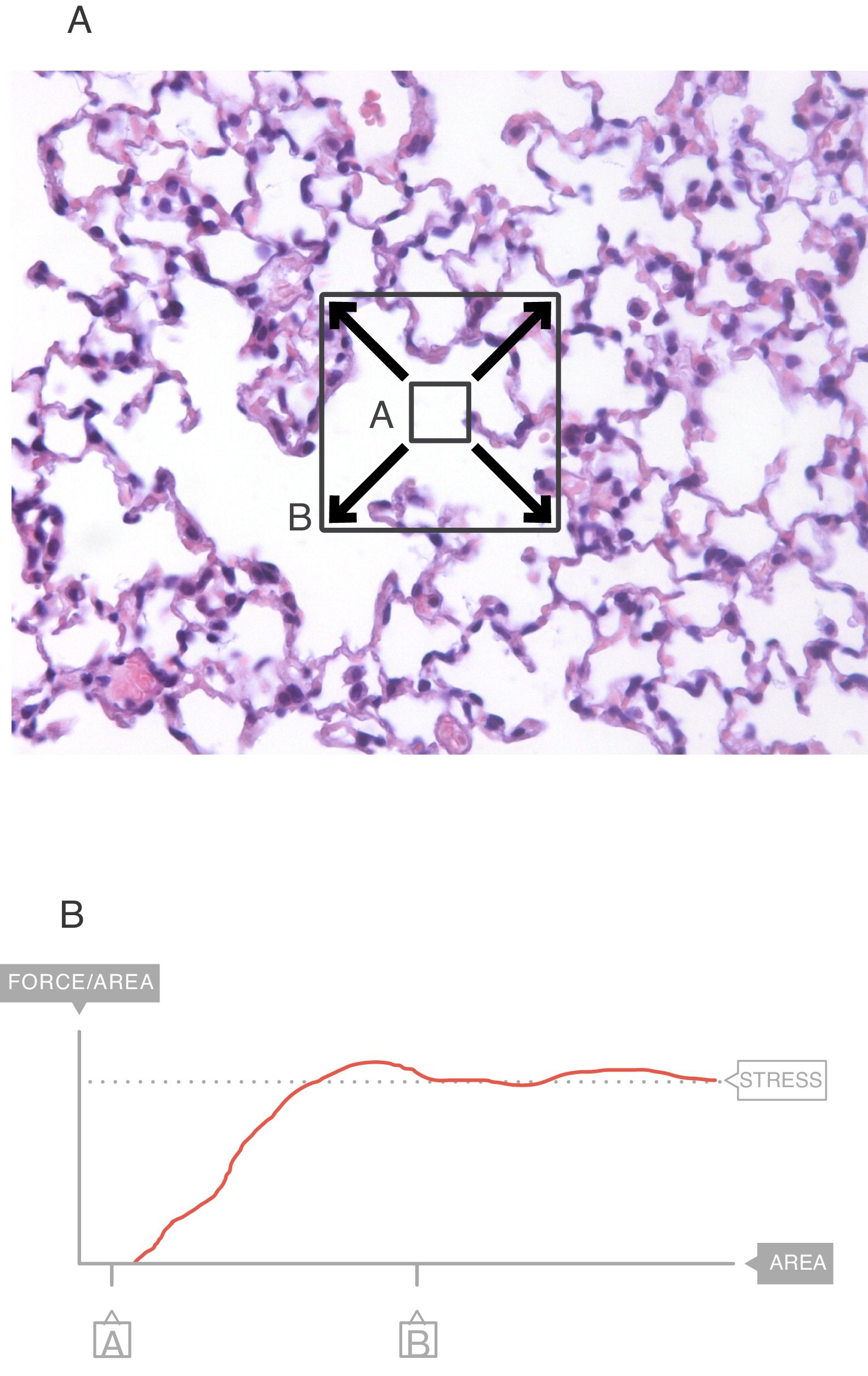
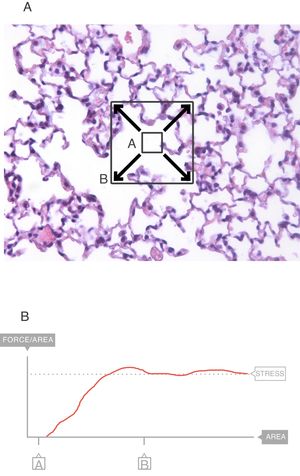
In the interior of the pulmonary parenchyma (Fig. 3A), the forces are transmitted through the tissues and the surface tension.4 Sections A and B represent the expansion of the lung tissue and the stress of this expansion can be measured. The maximum value (Fig. 3B) of this force can be referred to as the stress.6

Figure 3.

Stress=change in the retraction pressure of the lung (change in the transpulmonary pressure=ΔPTP). Source: Reproduced with permission Modesto-Alapont et al.5

(0.29MB).

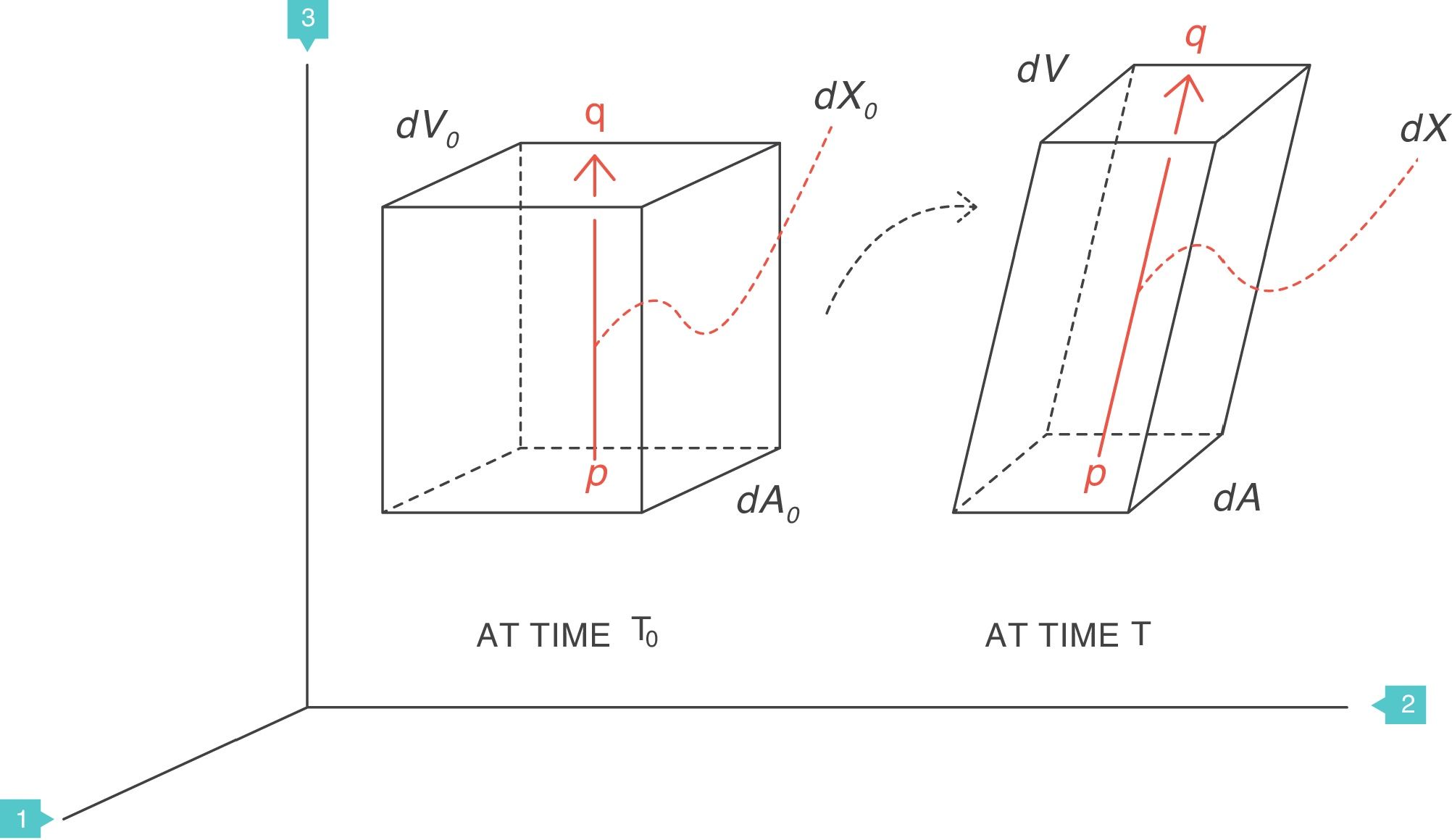
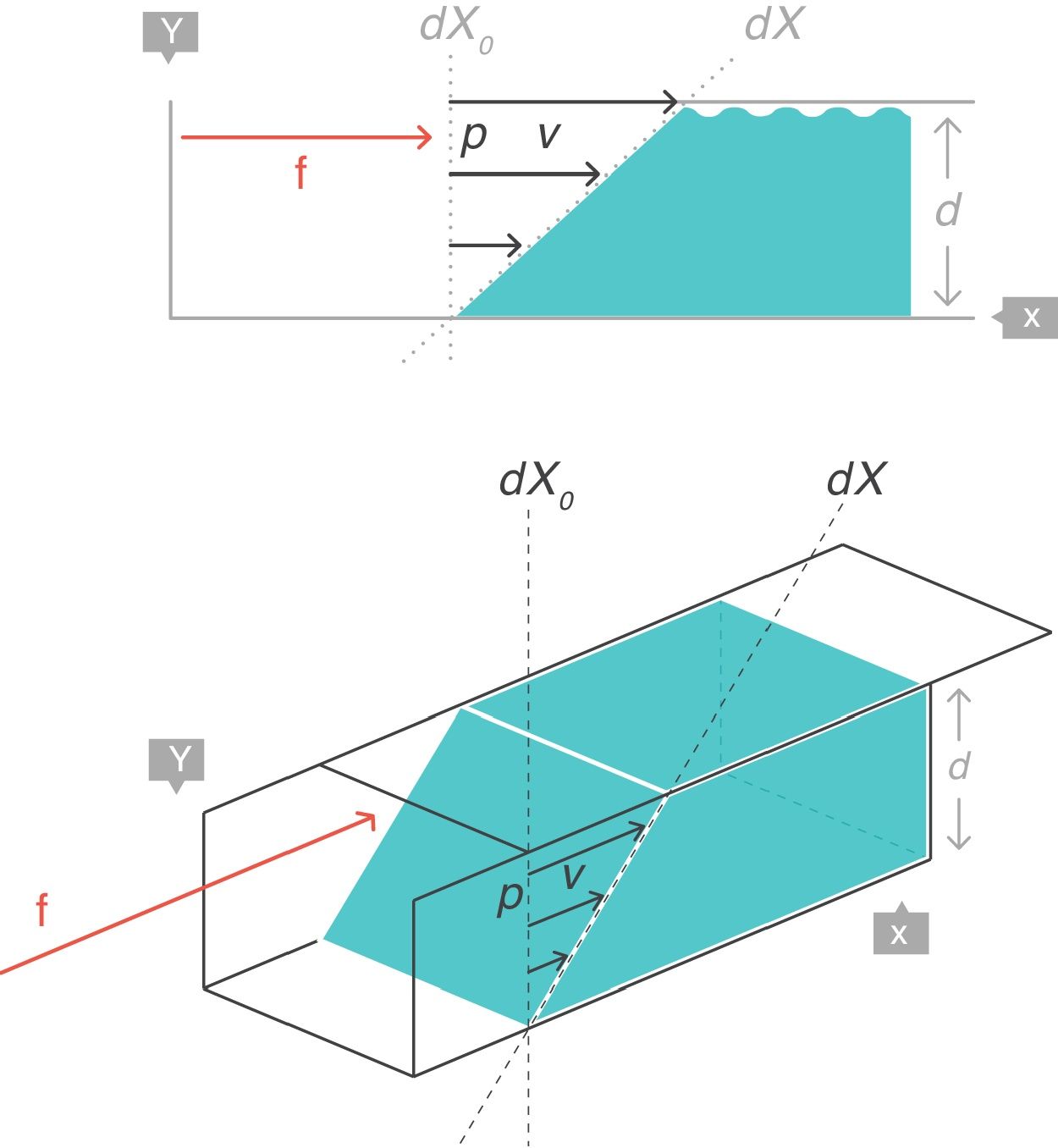
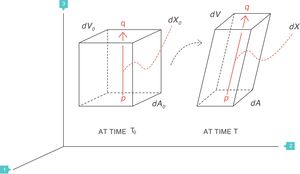
Supposing that inside a solid body, there are two points, p and q, separated by a distance dX0 (Fig. 4).3 On this body a force f is applied which deforms the body so that both points p and q are displaced from their original position. A new distance, dX, now separates them. The best way to describe these multi-dimensional changes is using “differential equations”. That is, the “deformation”, “relative displacement” or “strain” is the change in distance separating the two points p and q (dX−dX0) but relative to (divided by) the original distance dX0:

Figure 4.

Strain=deformation (tidal volume/functional residual capacity). Source: Reproduced with permission Modesto-Alapont et al.5

(0.08MB).

What is described above is the same concept as in a “zoom lens” of a camera or when using a smart phone and two fingers are used to expand a map. The strain is represented by the magnification power.

The deformation is a local physical phenomenon that appears close to the points inside the solid. The force that deforms the solid causes it to change the “scale” of its dimension: it produces a displacement (difference in distances). Therefore, the deformation only occurs if displacement is defined as a function of the original distance. In terms of mathematics, the deformation is the derivative of the displacement with respect to the original distance. The concept can easily be generalised to two dimensions (areas, dA), three dimensions (volumes, dV) or more spatial dimensions.

It is important to understand that strain is dimensionless i.e. has no units. Strain has a positive value when the applied force causes the solid object to become larger (expansion) and is negative when the solid contracts. This magnitude depends on both the displacement or gradient of distances (numerator) and the original shape of the body (denominator).

In classical respiratory physiology, the concept of “strain” does not exist. This strain concept or, deformation, could be called tidal volume (VT) which is the difference between the end-inspiratory volume and the end-expiratory volume.

The functional residual capacity (FRC) is comparable to the original distance (dX0). FRC is the volume of air that is filled by the respiratory system at the end of expiration. Therefore, in the respiratory system, strain is defined as:

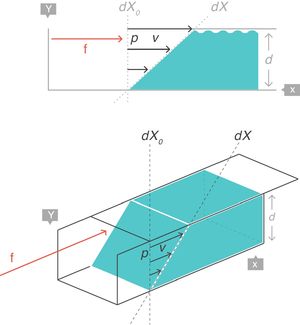
Now consider a thin film of a liquid body that is contained between two parallel metal plates and separated by a distance, d (Fig. 5).3 A force, f, is applied to this liquid body for a time dt. This causes the “upper slice” of the liquid to move relative to the remainder with a constant velocity such that it travels in time (dt) a distance (dX−dX0).

Figure 5.

Strain rate=velocity of the deformation. Source: Reproduced with permission Modesto-Alapont et al.5

(0.07MB).

This change of configuration of the liquid can be expressed again using differential equations. In this case, the “strain rate” is the velocity that the “upper slice” of the force-driven liquid has acquired but relative to the original position dX0 that it occupied in the liquid (which is that of the “lower slice” which has remained motionless).

Therefore, strain is the displacement relative to the original distance. The strain rate expresses the different velocities of displacements, in other words, the spatial gradient in velocities of displacements. The concept can be applied to one (length, dX), two (areas, dA), three (volumes, dV) or more spatial dimensions.

Strain rate has units of s−1. Strain rate only has a value when movement exists (zero value when the rate of deformation is zero, i.e. at rest). The magnitude of the strain rate depends on the velocity of the deformation (numerator) and on the original shape of the body (denominator).

In classical respiratory physiology, the concept corresponding to the strain rate does not exist either. Air flow is the quotient between the VT and the time needed for inspiration and expiration (t). So, in terms of classical physiology, the strain rate of the respiratory system is defined as:

Rheology uses different tensorial experimental conditions to understand the behaviour of a solid body. These experiments apply an ever increasing force until there is a fracture in the solid body. The behaviour of a solid material can be described using a stress–strain curve of the material:

• •

  Solid materials differ from each other by the specific shape of their stress–strain curve.

• •

  The shape of the stress–strain curve of each material depends in turn on several factors such as the chemical composition, temperature, initial plastic deformity and strain rate.

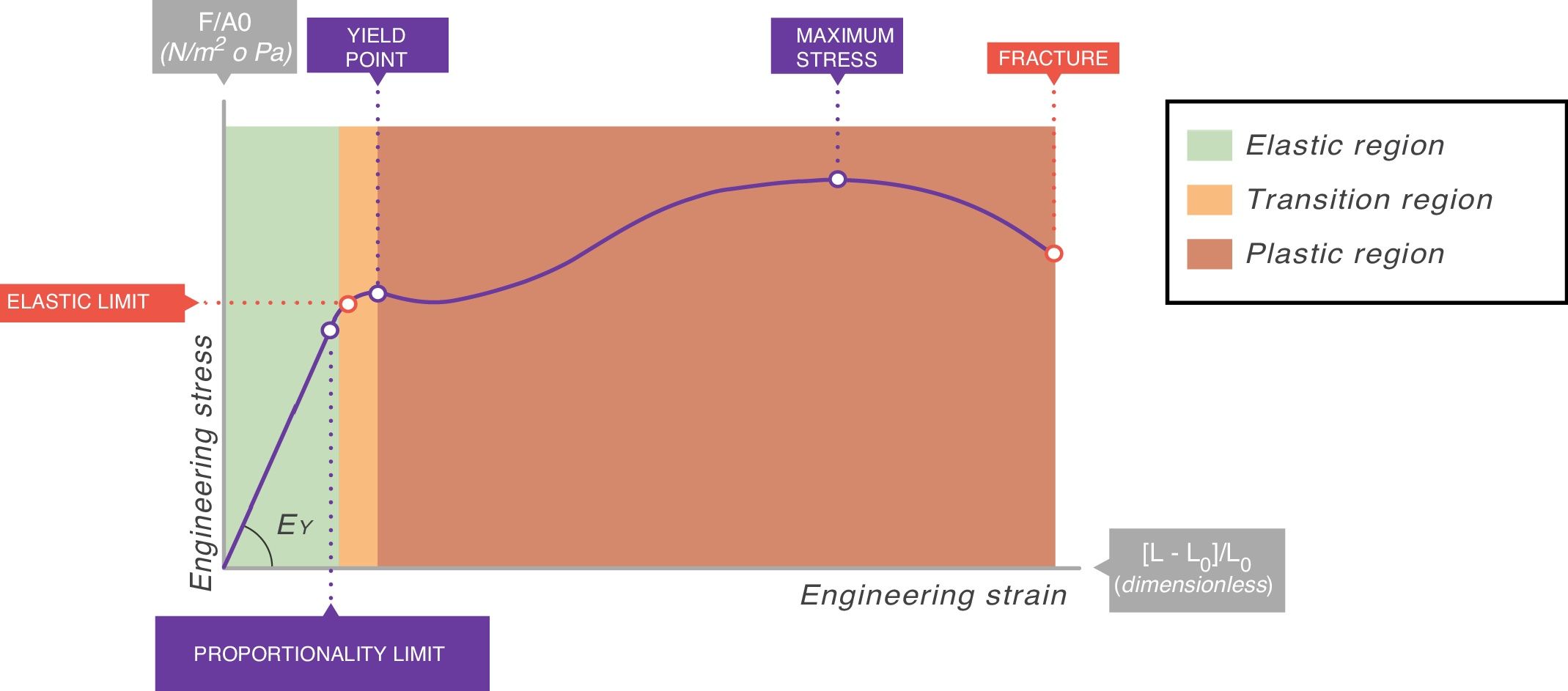
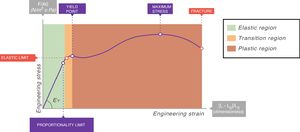
In all stress–strain curves, the initial phase is linear and this defines its elastic area (Fig. 6).7 The equation of this linear part is called the constitutive equation of an elastic solid (Hooke's Law):

Figure 6.

Stress–strain curve. EY: Young's modulus. Source: Reproduced with permission Modesto-Alapont et al.5

(0.08MB).

The proportionality constant (the gradient of the slope) EY is called Young's modulus of the solid. Young's modulus has a unit of pressure (stress is a pressure whilst strain is dimensionless) and is therefore, for our purposes, given units of cmH2O. The existence of Young's modulus is what defines the material: each solid has its own value of EY.

An ideal solid (which physicists call Hooke's solid body) is completely elastic: its stress–strain curve is completely and exclusively linear. If it is elastically deformed, the energy required for the deformation is stored within and its shape fully recovers when the applied stress is removed. If a solid is not perfect, the energy is only recovered completely in the elastic region (green area of Fig. 6). The majority of metals and ceramics under small deformations behave like Hooke's solid bodies. However, there are no ideal solids in nature.

In the stress–strain curve of all solids, beyond the elastic region begins a region of plastic behaviour (red area of Fig. 6) in which the deformation induces permanent deformity. Part of the energy is not fully recovered when the tension is removed. This portion of the applied energy is dissipated inside the solid and produces permanent structural changes in the original shape. “Lesions” or micro-fractures begin and produce plastic deformations. Beyond this plastic region, if the tension increases, the material fractures.

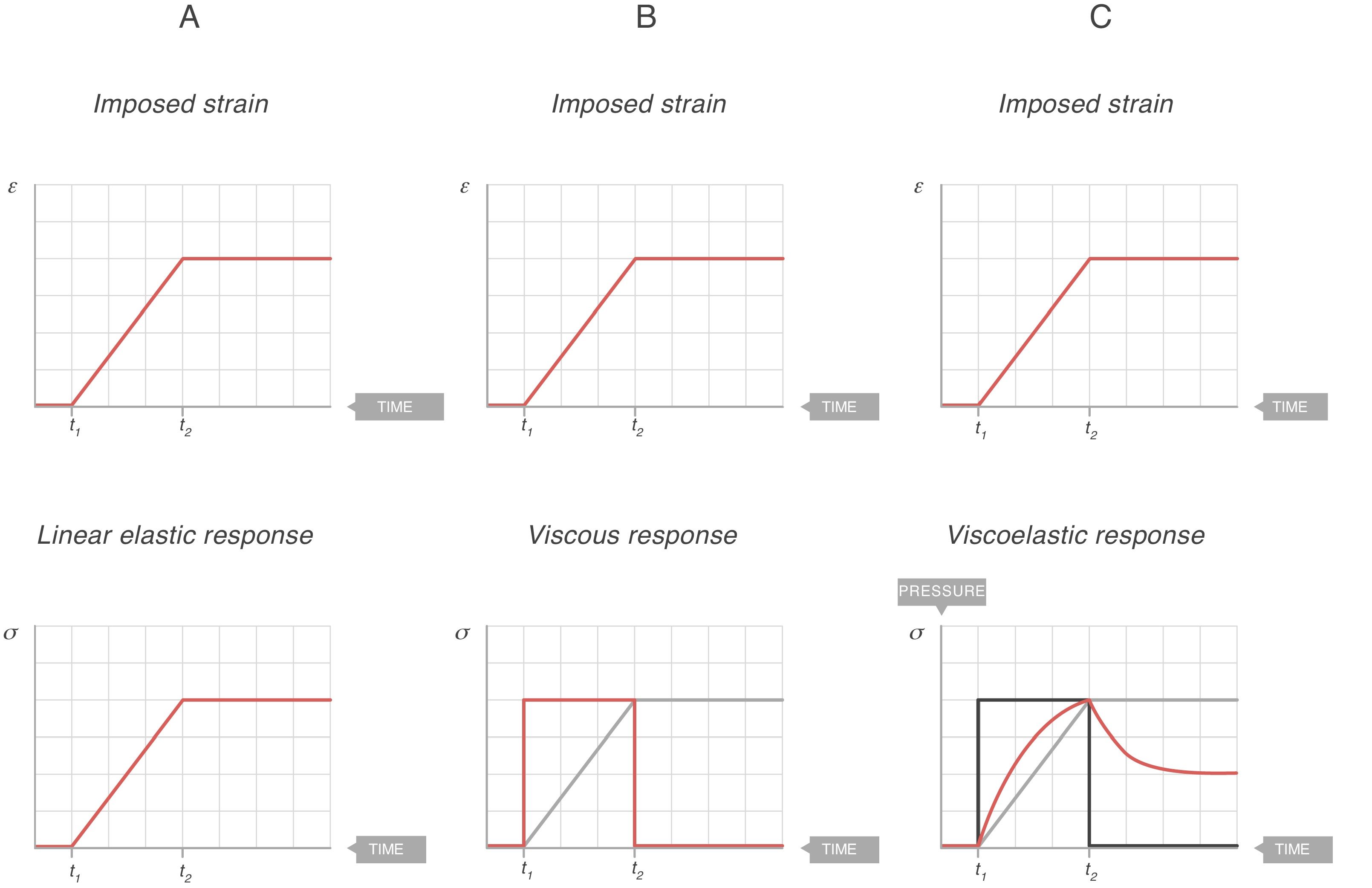
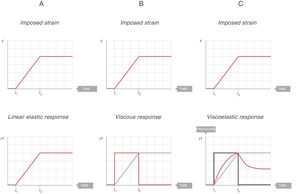
Fig. 7A shows the behaviour of an ideal solid. If during a time (t2−t1) a force is applied that produces a strain (above), it is observed that the stress supported by that body (below) is directly proportional to the produced strain. If the strain does not disappear, the stress does not decrease. So, in an ideal solid, strain and stress are directly proportional to each other.

Figure 7.

Elastic, viscous and viscoelastic behaviour. Source: Reproduced with permission Modesto-Alapont et al.5

(0.21MB).

In the case of liquid bodies, Rheology reveals how these bodies flow in response to the forces applied on them. In order to do this, Rheology studies the stress supported by the liquid when a force is applied and the strain rate. Remember that strain rate is a derivative of the strain with respect to time.

A perfect ideal liquid (which physicists call Newtonian fluids) behaves according to the constitutive equation of a liquid:

The constant η is the viscosity modulus of the liquid (cmH2O×s). The existence of viscosity modulus is what defines the liquid: each liquid has its own value of η.

Fluids behave quite differently from solids. When a force is applied to an ideal liquid, the stress supported by the liquid causes it to deform irreversibly. The energy required for the deformation is completely dissipated in the form of heat and entropy and cannot be recovered when the force is withdrawn.

Fig. 7B shows the behaviour of an ideal liquid. If during a time (t2−t1) a force is applied that produces a deformation in a body (above), it can be seen that the stress supported by that body (below) behaves in a totally different way to what happened in a solid. It is not directly proportional to the strain produced, but is directly proportional to the strain rate, at the speed with which the deformation has occurred. Since, in this example, the strain is a linear function, the velocity of that strain is a derivative of this linear function: it is constant for the duration of the movement. Therefore:

• •

  Only when the liquid is moving is it under stress and this stress is constant.

• •

  When the movement ceases, the stress supported by the liquid becomes zero.

• •

  The energy required for deformation has been spent heating the liquid and causing it to flow.

The majority of materials in nature display a behaviour in between that of solids and liquids. In fact, they have both elastic and viscous properties at the same time. This is the reason why they are called viscoelastic bodies.

In Rheology, viscoelastic behaviour can be explained using different systems: Maxwell body, Kelvin body, etc. The model that best explains the biophysical behaviour of the respiratory system is the eight-parameter model of Bates,8 however it is too detailed to be discussed here.

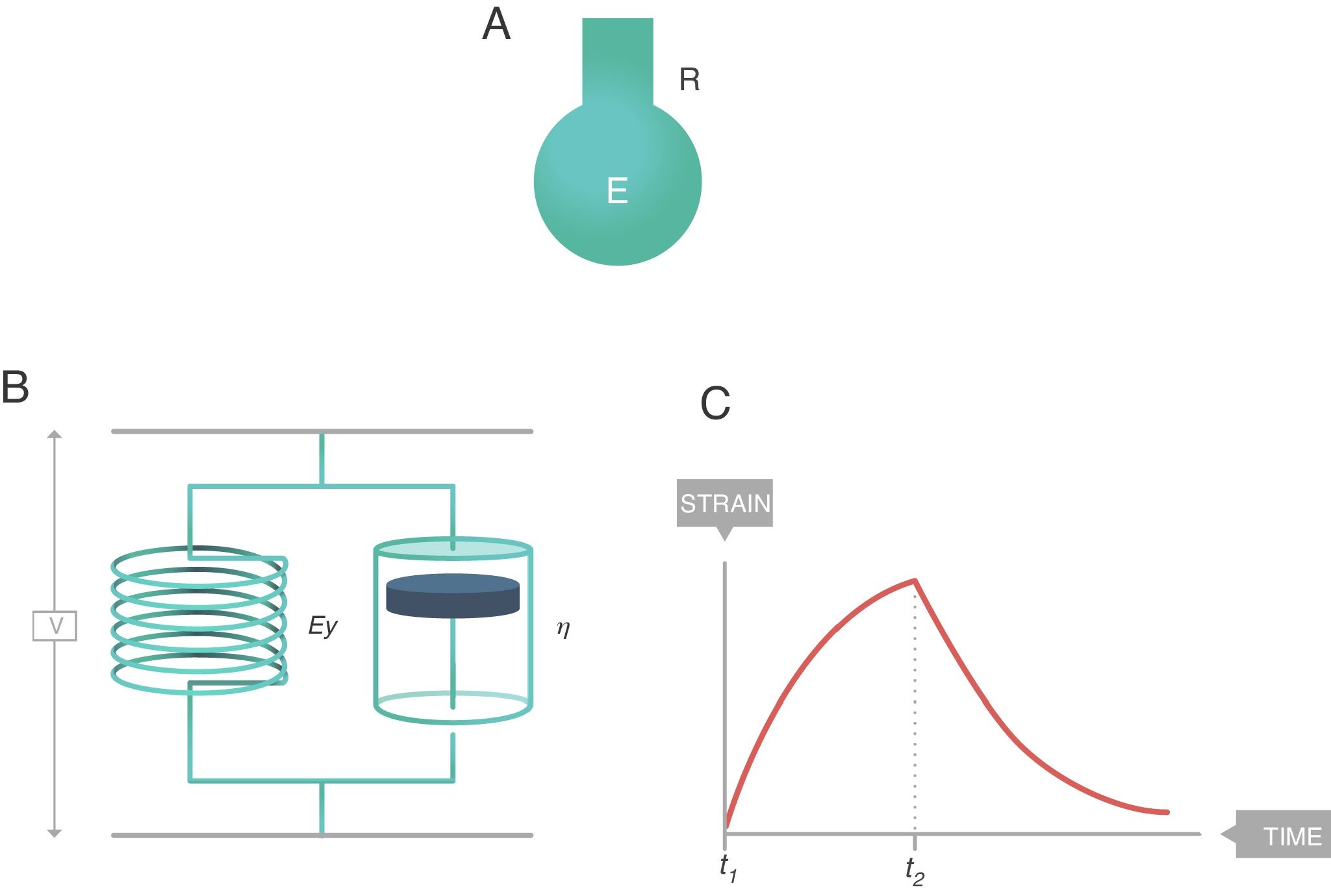
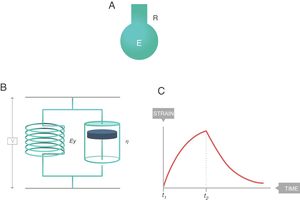
The simplest way to describe viscoelastic bodies with sufficient accuracy to be used in clinical practice is the Voigt solid body (Fig. 8), formed by a spring (modulus of elasticity, EY) and a damper (viscosity modulus, η) which are connected in parallel. In this Voigt viscoelastic model:

• •

  The overall stress supported by the complete Voigt solid is the sum of the stresses borne by each of its components.

• •

  The strain induced in each of the components is the same and equal to the strain induced throughout the Voigt solid.

Figure 8.

Voigt solid body. E: elastance; R: resistance; EY: Young's modulus; η: viscosity modulus. Source: Reproduced with permission Modesto-Alapont et al.5

(0.07MB).

There is also a constitutive equation of viscoelastic bodies. In the case of a Voigt solid, it is called the Voigt equation:

From this equation, it is possible to arrive at the following equation which governs the deformation in relation to time (t2−t1) of a Voigt body when stress is applied:

This equation is a function of the time constant or τ (s), the so-called time constant of the Voigt body, whose value is:

In Fig. 7C the behaviour of the viscoelastic body is shown.9 A viscoelastic body has a behaviour in between that of an ideal solid and ideal liquid:

• •

  If during a time (t2−t1) a force is applied that produces a deformation in a body (above), the behaviour of the stress supported by that body can be observed (below). As can be seen, during the time that there is movement, the body supports a stress (blue line) which is in between being a solid (proportional to the strain, Fig. 7A) and a liquid (proportional to the strain rate, Fig. 7B).

• •

  When the movement ceases, the stress produced by the strain rate disappears. That energy has been used to heat the body and has dissipated internally.

• •

  The total stress is in between a solid and a liquid (which would be zero).

This phenomenon is also modelled in the Voigt body (Fig. 8). Beyond the time (t2−t1) in which the force is applied, when the Voigt body is devoid of stress (stress relaxation) this viscoelastic system reverses the deformation with a strain loss that follows the equation:

This is easy to recognise in the profile of this figure and the red line in Fig. 7C. In a bedside situation, this is similar to the inspiratory phase of the pressure–time curve in a ventilator in a volume controlled mode. So, from the physical point of view, it is reasonable to assume that the respiratory system behaves like a viscoelastic body. In fact, in mechanical ventilation at least three phenomena have been described that are associated with the viscoelastic behaviour of the respiratory system:

• 1.

  Dynamic hysteresis (in the dynamic pressure–volume loop).10

• 2.

  Stress relaxation (difference P1–P2 after an inspiratory pause of 5s).11

• 3.

  The stress index.12

The classical physiology proposed to explain the working of the respiratory system,13 which is currently used to understand mechanical ventilation, assumes that during normal breathing energy is used to overcome two forces: resistive pressure and elastic pressure. This assumes that the behaviour of the respiratory system is governed by the so-called movement equation:

P(t) is the pressure applied by the ventilator, V(t) is the delivered tidal volume, F(t) is the flow to which that volume is delivered, which corresponds to the volume derivative with respect to time [F(t)=dV(t)/dt], and positive end-expiratory pressure (PEEP) is the pressure that exists in the airway at the end of expiration.14

This equation is a function of two constants: R, airway resistance to airflow, and E, pulmonary parenchyma elastance (or its inverse, compliance, C=1/E).

The product of C and R forms another constant, the time constant (τ=C×R=R/E) which represents the mechanics of the respiratory system. The resistive pressure is the pressure used to overcome R and this becomes zero when flow ceases.

Classical physiology has assumed that the respiratory system, whose constitutive equation is this equation of motion, could theoretically be modelled as a simple model called the “elastic-resistive body”).15 It is a theoretical body similar to the Voigt body. The elasticity of the spring (Young modulus coefficient or EY) is represented by the E of the pulmonary parenchyma. The coefficient of viscosity of the damper (η) is represented by R of the airway. When the system gains volume with a constant flow, the behaviour is reminiscent of a viscoelastic body: part of the applied energy dissipates inside the resistive element (R), while the other fraction of the total energy is accumulated in the elastic element (E) constituting the pressure necessary to exhale.

However, considering the equation of movement of the respiratory system, it looks similar but is not identical to the Voigt equation. In this equation it is necessary to include PEEP and:

• •

  The constant EY is replaced by E.

• •

  The constant η is replaced by R.

• •

  The strain has been replaced by the VT [V(t)].

• •

  The strain rate has been replaced by the flow [F(t)].

However, in rheology, strain is not the same as VT and strain rate is not the same as flow.

Therefore, answers to the following important questions can be considered:

• 1.

  Is the human respiratory system physically like a viscoelastic body?

• 2.

  And would it be possible for Rheology to offer a better explanation for VILI?

In 2011 Gattinoni16 made an exceptional discovery. In a case–control study experiment, pigs were artificially ventilated. The outcome variable was the autopsy presence of VILI after 60h of ventilation. Gattinoni et al. discovered the existence of a Young (EY) modulus in the respiratory system: a linear proportionality relationship between strain and stress. That is, he demonstrated that the respiratory system is rheologically, an elastic solid because the constitutive equation of a solid (Hooke's law) had been fulfilled. Using the rheological definitions of strain and stress and the classical concept of pulmonary elastance:

It can be calculated that:

Therefore:

This means that EY cannot equal E, and therefore the rheological model cannot be equal to the elastic-resistive classic model. It can be concluded that it is not possible to use the rheological model in a bedside situation. This is because FRC (necessary to measure the strain) and the pulmonary stress are difficult to measure. And there is no correlation between FRC and PEEP, or between ΔPTP and the VT(17).

Young's (EY) modulus of the respiratory system is called specific lung elastance (ESL). ESL in a healthy pig is 5.4±2.2cmH2O.

Considering this formula ΔPTP=EY×VT/FRC, ESL coincides with the PTP gradient that fills the lungs with a volume double that of FRC (i.e. produce the input of a VT equal in magnitude to the FRC, whereby the strain would equal 1). Conversely, it is called specific lung compliance (CSL), and it does not directly equate to the C of the classic model:

When looking at the stress–strain curve of a healthy pig lung, Gattinoni et al. further discovered that the direct proportionality between stress and strain is preserved for strain values less than 1, but the relationship begins to lose its linearity for strain values between 1.5 and 2. Rheology predicts, therefore, that from this elastic limit, VILI begins: the pulmonary deformation is no longer totally reversible and microfractures (established deformities) begin to occur. This prediction has been validated in this experiment and others. In Gattinoni's pigs, the probability of the presence of VILI increased exponentially with the strain value. When there was no VILI the strain value was 1.29±0.57 but on the other hand when VILI was present the strain value was 2.16±0.58 (p<0.001. More importantly, all the pigs without VILI survived, but the mortality of pigs presenting with VILI after only 60h of ventilation was 86%.

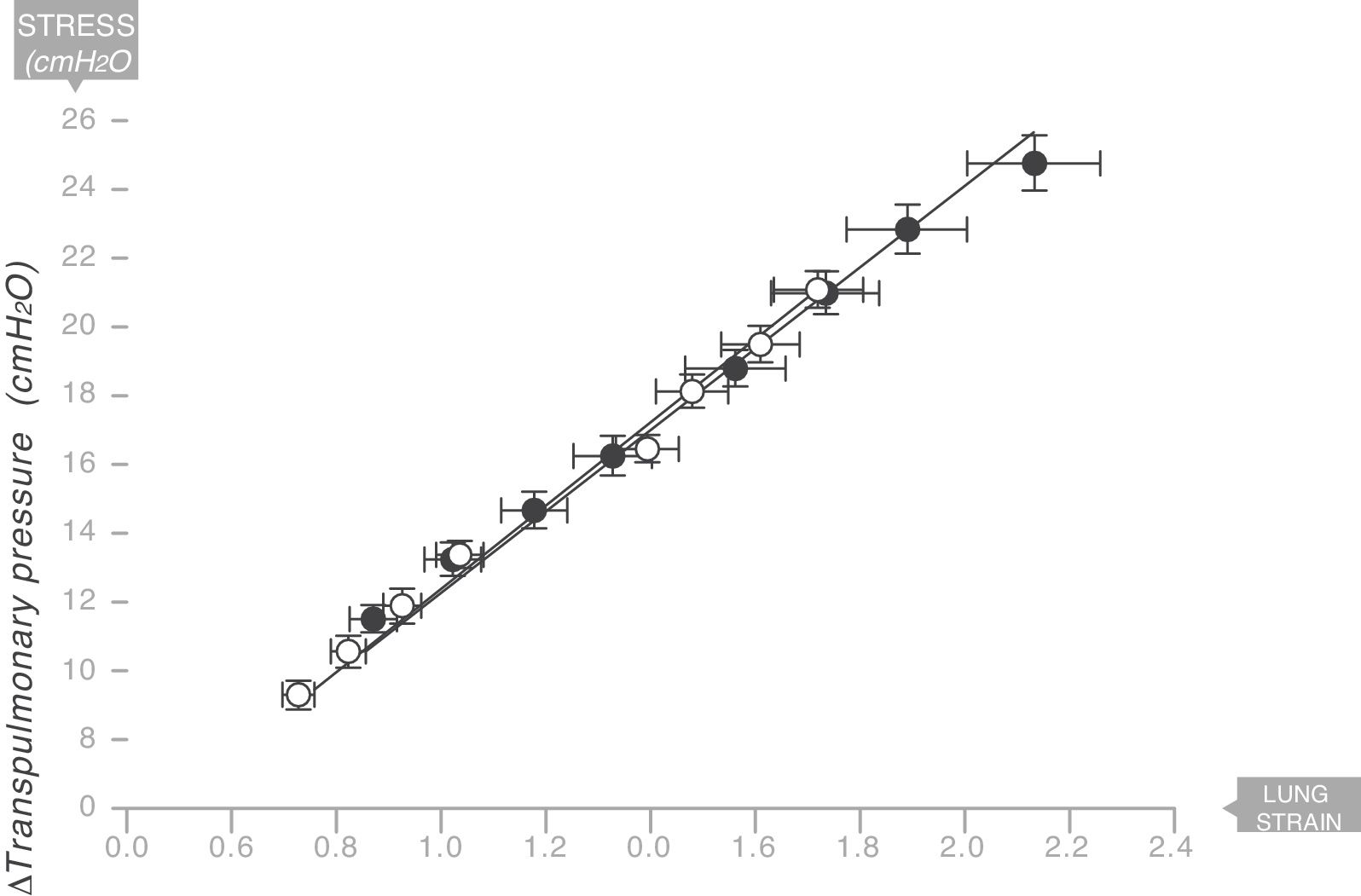
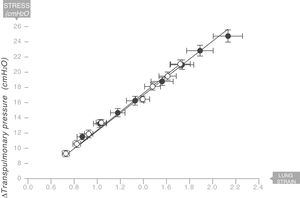
In 2008 the same team led by Gattinoni and Marini18 described the existence of a Young's modulus in the lungs of a series of acute respiratory distress syndrome (ARDS) patients who were under mechanical ventilation (Fig. 9). Therefore, the human lung can be classified as an elastic solid. The value of the specific elastance in the human adult lung with ARDS is ESL=13.5±4.1cmH2O (95% confidence interval [CI]: 11.8–15.2). This value is astonishingly constant regardless of the cause of ARDS, or the VT, or PEEP used in ventilation. In children with ARDS, the same team of researchers have found that the value of specific elastance in the paediatric lung is ESL=13.5 (95% confidence interval [CI]=10–15.3)cmH2O. This is therefore a value that does not appear to change, regardless of age.19

Figure 9.

Young's modulus in lungs of patients with acute respiratory distress syndrome (ARDS) (solid circles) and control patients (white circles). Specific elastance of the lung is equal to 13.5±4.1cmH2O. Source: Modified and reproduced with permission of Chiumello et al.18

(0.05MB).

In 2012 Spanish researchers led by Muñiz-Albaiceta found a direct correlation between the magnitude of induced strain by mechanical ventilation and IL-6 and IL-8 values in bronchoalveolar lavage.20 The FRC was measured using oxygen washing/washout methodology. All patients were ventilated with a VT of 7mL/kg. However, the group of patients ventilated with lower PEEP pressures (less air was present in their FRC at the end of expiration) and lower driving pressures (22.6±6cmH2O) suffered from greater pulmonary inflammation. This means that the barotrauma theory is not valid.

It seems to be that the rheological model and the classic elastic-resistive model are essentially paradigms. The main difficulty in finding the relationship between the two is the difficulty in measuring the value of FRC at bedside with a ventilator.

Marini et al. studied the relationship between the stress of the rheological model (ΔPTP [cmH2O]) and driving pressure (DP, cmH2O), which is the difference between plateau pressure (inspiratory pause) and total PEEP (expiratory pause).21 Both parameters are easy to measure. They found that:

• •

  The value of the ΔPTP/DP ratio in different clinical situations (including healthy lungs) varies between 0.46 and 0.79.

• •

  In patients with ARDS the value is 0.75.

• •

  Except in patients with ARDS the ΔPTP/DP ratio decreases as the intra-abdominal pressure increases.

• •

  The value of PEEP does not affect the ΔPTP/DP ratio.

By independently replicating these findings, Chiumello et al. have also found a very close correlation (R2=0.7, p<0.001) between stress and DP.17 In lungs with ARDS, stress corresponds to 73–85% of DP: ΔPTP/DP=0.73–0.85.

In conclusion:

• 1.

  Young's modulus (specific elastance) of the human lung with ARDS is approximately 13cmH2O.

• 2.

  When mechanical ventilation produces a strain ≥1, this strain will start to produce a clinically relevant VILI.

So, taking these into account, it is important that the lung should be ventilated with a ΔPTP less than 13cmH2O. Chiumello et al.17 demonstrated that it is possible to use a DP to determine if the lung is subjected to a harmful stress. A threshold value of DP of 15cmH2O, had a very good diagnostic accuracy (area under the curve [AUC]=0.864 [95% CI=0.8–0.93], sensitivity=0.9, specificity=0.78 of evidence in favour=7 decibans; weight of evidence against=−8 decibans) to detect that the lung is being subjected to a stress ≥12cmH2O, and therefore could be inducing VILI.

It seems that DP is the basic parameter that connects the classical physiological theory with the rheological model and achieves the relationship between these two paradigms. A threshold value of DP=15cmH2O, which in humans corresponds to a strain around 1, seems to mark the elastic limit above which VILI is induced.

In this sense, using the rheological theories, Rahaman22 explained clearly a clinical phenomenon: mechanical ventilation using common settings will not cause a clinically relevant VILI within normal lungs. Knowing that in the human healthy lung, the FRC is 35mL/kg and the TLC is 85mL/kg.23 If using a ventilatory strategy where the end-inspiratory lung volume is equal to the TLC and the end-expiratory lung volume is equal to the FRC, the stress is:

This stress level (ΔPTP) is equal to DP, so:

This value is clearly more than the DP threshold of 15cmH2O. Therefore, with this strategy (which induces a strain of 1.5) VILI would be caused in a healthy lung.

It is easy to deduce that in a healthy lung, using a ventilator strategy of VT of 6mL/kg (strain=0.17; stress=2.31cmH2O; DP=2.89cmH2O) or even a VT of 10mL/kg (strain=0.29; stress=3.86cmH2O; DP=4.82cmH2O) will not cause VILI in either circumstance. This was exactly the traditional strategy used in healthy lungs.

The main scientific evidence has been provided by a multinational team of researchers led by Amato et al.24 This was a meta-analysis of clinical studies published in 2015 in NEJM, which included 3562 ventilated patients with ARDS. They used statistical techniques (multilevel mediation analysis) to minimise the bias of confounding induced by prognostic factors known prior to the initiation of mechanical ventilation (e.g., arterial oxygen tension/inspired fraction of oxygen ratio [P/F] upon entering the trial). Of all the ventilator parameters, the DP in the first day of ventilation was one most associated with survival. For each increase in 7cmH2O in DP, the relative risk of death increased by 1.41 (95% CI=1.31–1.51, p<0.001). This effect was seen even in patients with lung protection therapy (RR=1.36 [95% CI=1.17–1.58, p<0.001). Changes in VT, Pplat or PEEP did not affect survival, unless a change in DP occurred.

In addition, in the LUNG SAFE cohort,25 the most consistent parameter associated with mortality is the use of a DP >14cmH2O. Its effect is shown in all the severity groups of ARDS.