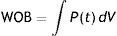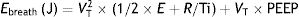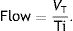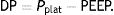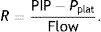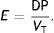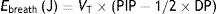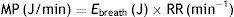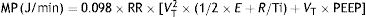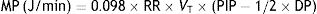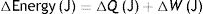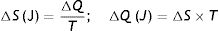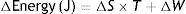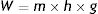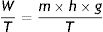Currently, the effect of PEEP on the incidence of VILI has not yet been established experimentally from the rheology perspective based on the effect of stress and strain.

Theoretically, since increasing PEEP increases FRC and it is a key element of strain and strain rate, increasing lung recruitment by increasing PEEP should decrease VILI, although there exists contradictory results.

Data from two studies point in this direction.10,11 However, it is difficult to predict the effect of PEEP on pulmonary recruitment12 at the bedside, as PEEP does not always increase FRC in patients with ARDS. This theory could be based on an erroneous and therefore a biased hypothesis.

The results of the clinical trials offer interesting results. Kassis et al.13 reexamined the data from their NEJM article in which an improvement in elastance and decrease in stress (ΔPTP) had been demonstrated in patients with ARDS who were ventilated with an oesophageal pressure-directed strategy. This improvement was seen in those patients whom received higher PEEP during the first day. A case–control re-analysis found that the survivors (at 28 days) had been ventilated during the first day with a driving pressure (DP) less than 13cmH2O, a statistically lower value than the DP received by the patients who died (around 15cmH2O).

The Swedish Karolinska team has provided the most robust scientific evidence of the beneficial effect of PEEP on the development of VILI to date. They repeated their “two-hit injury model” study5 but with a significant modification: they applied a recruitment maneouvre to identify the optimal PEEP. This was defined as 2cmH2O above the PEEP which maximised the dynamic compliance in a decremental maneouvre.14 The animals in the experiment were ventilated with an Open Lung Approach (OLA) strategy however, the rest of the parameters were maintained as in their previous experiment (volume-control mode, VT=6mL/kg, FIO2=0.5). The two study groups received respectively a RR of 20bpm and 40bpm. After 4–6h of ventilation, the biochemical and anatomopathological VILI markers were indistinguishable between the two cohorts (high and low RR). These results were similar to those found in the lower RR cohort of the previous experiment (ARDSnet). Therefore, it can be concluded that in ARDS, PEEP prevents VILI caused by high RR.

Protti et al.6 came to similar conclusions. Both the low strain rate and high strain rate cohorts showed lower relaxation stress (P1–P2 difference) when ventilated with PEEP=10cmH2O than with PEEP=0cmH2O (ZEEP). There seems to be no relationship (p=0.994) between the effect of PEEP and strain rate therefore PEEP appears to be an independent factor that decreases the viscous behaviour of the lung parenchyma when ventilated. It is not possible to determine causality based on those results but, as higher PEEP allows the ventilation of lungs with lower stress relaxation, it is possible to infer that it reduces VILI.

The definitive step in the development of a complete theory that draws from rheology and materials engineering in order to scientifically explain the production of VILI has been the introduction of the concept of mechanical power (MP) by the team of Gattinoni in 2016. It allows the integration of all the different ventilator parameters that have been described as co-factors capable of producing VILI (VT, pressures, frequency and flow) in a single physical quantity. The objective is to measure the mechanical energy that is transmitted to the respiratory system of the patient (airway+lung parenchyma) by the ventilator. All this energy expressed per time unit (J/min) is the MP.

For physicists, energy and work are interchangeable concepts. Energy is a measurement of “ability to perform a job”, and work is “energy transferred by a force”.

In classical physiology, respiratory work of breathing (WOB) during inspiration using constant flow ventilation15 is measured as:

This means that the work done by the ventilator within each cycle to introduce air into the respiratory system coincides with the area under the curve of the inspiratory limb of the pressure-volume dynamic loop, measured on the volume axis. This work is exactly the energy that the ventilator supplies to the patient's respiratory system in order to ventilate it. Based on this understanding, Gattinoni et al.16 obtained two formulae capable of estimating MP during volume control ventilation; these formulae are very easy to calculate. The formulae adapt the classical respiratory physiology equation of movement with a geometric model of the pressure–volume loop (available currently in most mechanical ventilators) (Fig. 1).17 The energy supplied (J) in each cycle using a constant-flow modality is:

Figure 1.

Mechanical power calculation. From a practical point of view, the elastic triangle (green triangle) is not included in the energy calculation because this energy is only used in the first inspiration. The key point is the energy which is delivered in the following consecutive breaths. PEEP: positive end-expiratory pressure; Ebreath: energy supplied in each breath; VT: tidal volume; Pplat: plateau pressure; PIP: peak inspiratory pressure; DP: driving pressure.

(0.24MB).

This equation is calculated in relation to two constants, elastance (E=1C−1) and resistance (R), but it can be simplified if we know that:

Applying those concepts, it is possible to simplify the formula to:

Multiplying the energy supplied in each cycle by the RR mechanical power can be calculated:

As 0.098 is the conversion factor from L (from VT)×cmH2O (from the pressure) to Joules:

Or its simplified equivalent:

In this article, Gattinoni demonstrated that the resulting calculation of these formulae is equivalent to the area under the curve of the dynamic pressure–volume loop, on the volume axis (work of breathing), both in normal lungs and in patients with ARDS. Using computer simulation models he also concluded that:

• •

  MP increases exponentially:

  • ∘

    With VT, DP and Flow (exponent=2).

  • ∘

    With RR (exponent=1.4).

• •

  MP increases linearly: with PEEP, E and R.

In the same year, the same research team published18 a proof of concept study that concluded that MP is the cause of VILI. That study consisted of two experiments.

• •

  The first experiment identified a MP threshold above which VILI is produced. They studied mechanically ventilated pigs, ventilated in volume control for 54h with a strain ≥2 (previously thought to develop VILI and cause death at RR of 15bpm) and divided them into 5 cohorts. Each of the cohorts was ventilated with a different RR (3, 6, 9, 12 and 15bpm), producing different mechanical powers (2±0.2J, 7±3J, 10±3J, 14±2J and 22±2J). The production of VILI was identified using CT scan and with histology. Only when MP was greater than 12J/min was VILI produced. Below that threshold, there was no pathology. The experiment was shortened due to the death of the pigs ventilated at higher MP.

• •

  The second experiment was a confirmation experiment to demonstrate that RR is not the single factor in the production of VILI. This time, all pigs were ventilated at 35bpm for 54h and divided into two cohorts based on the effects of VT on MP. In the first group the MP was less than 12J/min (8±2J/min) and in the other group, MP was greater than 12J/min (22±5J/min). The results confirmed the findings of the first experiment: VILI was induced in the high MP cohort, where stress, strain, Ebreath, and dynamic hysteresis rates increased during MV (i.e. the duration of ventilation worsened VILI).

In addition, data from both experiments demonstrated that the MP supplied is inversely proportional to the oxygenation drop (P/F) and directly proportional to the increase in elastance, viscous behaviour indexes (P1–P2 difference, dynamic hysteresis) and the anatomopathological measures of pulmonary injury.

The existence of this MP threshold is an extremely relevant finding and is compatible with what is already known in material science.19–21 In any material, there are always impurities (sometimes microscopic) that act as stress raisers and contribute to the formation of internal fractures. From these initial points of rupture, the extension of fractures follows the so-called Griffith fracture criterion where the energy has to increase over a certain threshold to propagate the fracture. This extension produces fatigue within the material. The analogy of this theory with MP and VILI is clear.

The scientific evidence of the role of MP in VILI development is still not very robust but it points strongly in that direction. In the LUNG SAFE22 cohort, the use of PEEP was independently associated with decreased mortality, and elevated RR, PIP and DP increased mortality. All those parameters are included in the abbreviated formula of MP.

Another study by Fuller et al.23 found that in patients with healthy lungs in which a protective ventilation strategy was applied, both increased DP and MP were associated with the development of ARDS.

The identification of a MP threshold from which VILI is generated seems to be very relevant for strategies at the bedside.

The use of high frequency oscillation ventilation (HFOV) seems to be a paradigmatic everyday example. Based on volu/barotrauma theories, the use of HFOV should be safer and less harming than conventional mechanical ventilation (CMV) as VT is delivered below dead space with a moderate continuous distending pressure (MAP). Contrary to that theory, the current available literature has not demonstrated superiority and has even shown worse outcomes when using HFOV against CMV. This paradox can be explained by the energy transmission in HFOV. As the modality uses simple harmonic motion to deliver ventilation, the energy transmitted by this wave can exceed the MP threshold for VILI formation.

This assumption, based on the new theory, is only a hypothesis awaiting experimental confirmation. The same principles may, in the future, be used to refine the criteria for respiratory ECLS in patients with ARDS.

Aside from all these studies, Oliveira et al.24 published an alternative version of the same theory from the point of view of thermodynamics. Thermodynamics is the part of physics that deals with the mechanical action or relations to heat. For a better understanding, it is necessary to consider that a lung that is artificially ventilated does obey the laws of thermodynamics as it transitions from one state (expiration) to another (inspiration) and vice versa. To understand this reasoning, it is only necessary to understand the first two laws of thermodynamics:

• •

  First law of thermodynamics. This is the law of conservation of energy. Energy cannot be created or destroyed, only changed in form. This applies to the internal energy of a thermodynamic system and how it changes. According to this law there are only two ways of changing the internal energy of a closed, i.e. one that is unable to exchange matter, thermodynamic system:

  • 1.

    Heating it (or cooling it) with a certain amount of thermal energy (Q).

  • 2.

    Doing work (W).

    
    Q: thermal energy; W: work.

• •

  Second law of thermodynamics. In a repeated process, there will always be some energy that cannot be converted into work. This explains the generation of entropy (S), which is the amount of thermal energy that cannot be converted into work. When a change of state occurs, the entropy of a system can never decrease. If entropy has to be calculated in relation to absolute temperature (in Kelvin degrees), this formula must be used:

  
  S: entropy; T: temperature; Q: thermal energy.

  Combining both laws, the equation for the state of a thermodynamic system is obtained:

  
  S: entropy; T: temperature; W: work.

This equation describes the relationship between internal energy, temperature, entropy and the work done by (or on) a thermodynamic system.

The essence of a living being is a continuous internal activity of an extremely organised nature (electrical, chemical and temperature gradients). In 1944, the book “What is life?” by Erwing Schrödinger stated that, from the thermodynamic point of view, living beings are able to maintain order throughout their lives in an apparent violation of the second law of thermodynamics. For that, they must be able to transfer to the environment around them the entropy they are generating. However, what happens if not all the entropy can be exported? The remaining entropy is retained within the system and its inevitable consequence is the gradual progression of the system towards dysfunction (i.e. illness) and eventual death. This raises two essential questions about the life and death of an organism: at what rate is entropy produced within an organism and how effective is that organism at exporting the entropy generated? This philosophical explanation has been considered at a lung level by Oliveira et al.

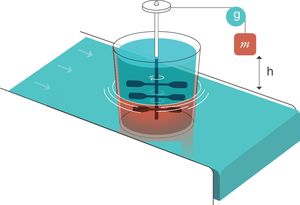
For thermodynamics,25 an entropy generator is a system composed of two parts that are in contact. This is an example (electronic Fig. 2):

• 1.

  The first part is a weight of mass m that is submerged in a viscous liquid and is falling inside it. During the fall, it rotates a set of paddles.

• 2.

  The second part is a heat reservoir that maintains a constant temperature T and is in thermal contact with part 1. For thermodynamics, a “heat reservoir” is capable, by definition, of keeping the temperature constant regardless of how much it is heated or cooled. It has an infinite capacity to absorb heat.

Figure 2.

Entropy generator. Reproduced with permission Modesto-Alapont et al.17

m: mass; h: distance; g: gravity.

(0.05MB).

When the mass of weight m falls (because of the effect of gravity, g) a distance h, a work W is done on the inside of the viscous liquid:

This produces an increase in the thermal energy of the viscous liquid which would lead to an increase in its temperature because of the existence of the heat reservoir. Since the liquid and the reservoir are in thermal contact and the reservoir maintains its constant temperature, when the weight drops, the liquid transfers that energy in the form of heat to the reservoir thus causing the entropy of the reservoir to increase.

If the liquid is able to transfer that entropy to the reservoir, its entropy remains constant. The “entropy generator” demonstrates that when a work (W) is completely dissipated in a heat reservoir of temperature (T), the entropy of the complete system (liquid+reservoir) increases by a quantity (W/T).

The system formed by the lung and the circulatory system can be described as an entropy generator:

• 1.

  Respiratory system. The liquid moved by the paddles would represent the lung subjected to the respiratory work (WOB=Ebreath) produced by the mechanical ventilator in every inspiration. It is important to remember that the mechanical power (MP) is the energy multiplied by the respiratory rate.

• 2.

  Circulatory system. This system acts as the calorific reservoir that is in thermal contact with the lungs and is able to maintain constant body temperature (isothermal conditions at 36.5°C, 273.15±36.5°C=309.65°K).

As long as the lung is able to export the entropy to the circulatory system, dissipating completely the work done on itself, the pulmonary entropy remains constant: VILI will not be produced. However, if the MP is too high and exceeds the capacity of the circulatory system to remove the entropy that is occurring inside the lung, part of the entropy generated (MP/T) produces VILI in the lung. Therefore, the ability of the circulatory system to eliminate entropy generated inside the lung explains why there is a threshold of MP from which VILI is generated.

Oliveira et al. postulated that if the lung moves within the elastic limit (with a small strain), the three-dimensional distribution of the microscopic fibres of elastin and collagen of the interior of the lung tissue causes the stress to fall almost exclusively on the elastin fibres. Elastin fibres have a very characteristic thermodynamic property: they behave like elastic rubber bands and have a Young's modulus proportional to their absolute temperature (T). This means that:

• •

  When they are stretched during normal breathing (inspiration) they are able to release heat to the environment that surrounds them (circulatory system), decreasing their entropy.26

• •

  During contraction (expiration), they can recover the thermal energy from the circulatory system and transform it into work thus returning the system to equilibrium.

If the lung is ventilated, applying energy (MP) in the range where the lung behaves like an elastic solid, all the energy provided during inspiration is recovered at the end of expiration without losses. Entropy is not generated. The process is reversible and VILI does not occur.

On the other hand, if the amount of energy applied turns the lung into a viscous liquid, the mechanism of the “entropy generator” starts. In this case, stress also falls on the collagen fibres which are approximately 100 times more rigid than elastin and hyaluronic acid, one of the weakest structures of the extracellular matrix of the lung.

As long as the circulatory system is capable of removing the entropy (MP/T) generated inside the lung, VILI is not produced. However, if the MP is too high and the capacity of the circulatory system to withdraw is saturated, then the entropy irreversibly deforms the parenchyma and produces VILI.

Knowing that:

• •

  The hyaluronic acid molecular weight is 2500Da.

• •

  The human lung possesses 0.1×10−6g of hyaluronic acid for each gram of lung tissue.

• •

  The force needed to break the bonds between hyaluronic acid and its surrounding proteins is (40±11)×10−12N.

Gattinoni et al.27 calculated that to displace the hyaluronic protein's bond by 2.8×10−6m, 1.12×10−16J are needed.

When MP is 12J/min, the entropy generated at 36.5°C is 12/309.65°K=0.038J/min. If the entropy is divided by number of molecules of hyaluronic acid affected, the energy applied to each molecule is approximately the same as the necessary energy to break their bond with the proteins. It is likely that each respiratory cycle is breaking a higher number of molecules than those that can be repaired physiologically. If MP increases, and with it the entropy divided by molecules, the rhythm at which fractures are generated exceeds the physiological capacity for repair and VILI is produced.

A new theory to explain VILI has been developed in recent years based on the knowledge of the physical changes generated by rheology, material science and thermodynamics. It has been evaluated experimentally in animal models but also, when the concept is applied to existing studies in mechanically ventilated humans, it can explain the facts and phenomena described in those patients more completely than the more established theories (barotrauma, volutrauma, atelectrauma and biotrauma).

The main component is the existence of an energy (MP) threshold above which VILI will be generated. In the near future, this is likely to revolutionise the indications and application of different modes of MV and may inform the thresholds for consideration of extracorporeal respiratory support.

The authors declare that they have no conflicts of interest.